UPW2G4R7MPD 摩根定律去掉非号
发布时间:2019/10/9 20:50:38 访问次数:2309
UPW2G4R7MPD为了简化,常用最小项下标编号来代表最小项,故上式又可写为L(A,B,C)=∑m(1,3,6,7)
例2.2.1 将逻辑函数L(A,B,C)=(AB+AB+C)AB转换成最小项表达式。
解:可经下列几步:
多次利用摩根定律去掉非号,直至最后得到一个只在单个变量上有非号的表达式,即
L(A,B,C)=(AB+AB+C)AB=(AB+AB+C)+AB
=(AB・AB・C)+AB=(A+B)(A+B)C+AB
利用分配律消去括号,直至得到一个与一或表达式
L(A,B,C)=(A+B)(A+B)C+AB
=⒕BC+ABC+AB
在所得式子中,有一项AB不是最小项(缺少变量C),则用(C+C)进行配项,可得
L(A,B,C)=ABC+ABC(C+C)
=ABC+ABC+ABC+ABC
=M3+M5m+M7+∑M(3.5.6.7)
由此可见,任一个逻辑函数经过变换,都能表示成唯一的最小项表达式。
卡诺图的引出,一个逻辑函数的卡诺图就是将此函数的最小项表达式中的备最小项相应地填人一个特定的方格图内,此方格图称为卡诺图。因此,卡诺图是逻辑函数的一种图形表示。
下面从讨论一变量卡诺图开始,逐步过渡到多变量卡诺图。
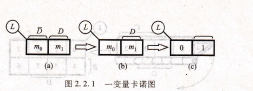
大家知道,n个变量的逻辑函数有2n个最小项,因此1个变量的逻辑函数有2个最小项。设变量为D,则1个变量的2个最小项是D和D,分别记为M0=D,m1=D。这两个最小项可用两个相邻的方格来表示,如图2.2.1(a)所示。方格上的D和D分别表示原变量和非变量。为了简明起见,非变量D可以不标出,只标出原变量D,即可得图2.2.1(b)。图2.2.1(c)所示是进一步的简化画法,其中mO、m1只用其下标编号来表示。
如果逻辑函数的变量为C、D,则二变量逻辑函数的最小项有22=4项,分别为mO=cD,%=CD,m2=CD,”3=CD。由于有4个最小项,可用4个相邻的方格来表示。
UPW2G4R7MPD为了简化,常用最小项下标编号来代表最小项,故上式又可写为L(A,B,C)=∑m(1,3,6,7)
例2.2.1 将逻辑函数L(A,B,C)=(AB+AB+C)AB转换成最小项表达式。
解:可经下列几步:
多次利用摩根定律去掉非号,直至最后得到一个只在单个变量上有非号的表达式,即
L(A,B,C)=(AB+AB+C)AB=(AB+AB+C)+AB
=(AB・AB・C)+AB=(A+B)(A+B)C+AB
利用分配律消去括号,直至得到一个与一或表达式
L(A,B,C)=(A+B)(A+B)C+AB
=⒕BC+ABC+AB
在所得式子中,有一项AB不是最小项(缺少变量C),则用(C+C)进行配项,可得
L(A,B,C)=ABC+ABC(C+C)
=ABC+ABC+ABC+ABC
=M3+M5m+M7+∑M(3.5.6.7)
由此可见,任一个逻辑函数经过变换,都能表示成唯一的最小项表达式。
卡诺图的引出,一个逻辑函数的卡诺图就是将此函数的最小项表达式中的备最小项相应地填人一个特定的方格图内,此方格图称为卡诺图。因此,卡诺图是逻辑函数的一种图形表示。
下面从讨论一变量卡诺图开始,逐步过渡到多变量卡诺图。
大家知道,n个变量的逻辑函数有2n个最小项,因此1个变量的逻辑函数有2个最小项。设变量为D,则1个变量的2个最小项是D和D,分别记为M0=D,m1=D。这两个最小项可用两个相邻的方格来表示,如图2.2.1(a)所示。方格上的D和D分别表示原变量和非变量。为了简明起见,非变量D可以不标出,只标出原变量D,即可得图2.2.1(b)。图2.2.1(c)所示是进一步的简化画法,其中mO、m1只用其下标编号来表示。
如果逻辑函数的变量为C、D,则二变量逻辑函数的最小项有22=4项,分别为mO=cD,%=CD,m2=CD,”3=CD。由于有4个最小项,可用4个相邻的方格来表示。



 公网安备44030402000607
公网安备44030402000607





