MB3771PF-G-BND-NH-ER 逻辑函数的最小项表达式
发布时间:2019/10/9 20:41:49 访问次数:1351
MB3771PF-G-BND-NH-ER观察表2.2.1可以看出,最小项具有下列性质:
对于任意一个最小项,输人变量只有一组取值使得它的值为1,而在变量取其他各组值时,这个最小项的值都是0。
不同的最小项,使它的值为1的那一组输人变量取值出不同。
对于输入变量的任一组取值,任意两个最小项的乘积为0。
对于输人变量的任一组取值,全体最小项之和为1。
最小项的编号,最小项通常用%表示,下标i即最小项编号,用十进制数表示。将最小项中的原变量用1表示,非变量用0表示,可得到最小项的编号,以ABC为
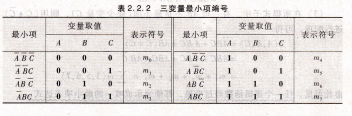
例,因为它和011相对应的最小项,而011相当于十进制中的3,所以就称ABC记作M3,是和变量取值011相对应的最小项,3,所以把ABC记作m3。按此原则,3个变量的最小项符号如表2.2.2所示。
逻辑函数的最小项表达式,利用逻辑代数的基本公式,可以把任一个逻辑函数化成若干个最小项之和的形式,称为最小项表达式。
例如,逻辑函数L(A,B,C)=AB+AC不是最小项表达式,利用A+A=1的基本运算关系,将逻辑函数中的每一个乘积项都化成包含所有变量A、B、C的项,即
L(A,B,C)=AB+AC=AB(C+C)+AC(B+B)
=ABC+AB C+ACB+AC B
此式由四个最小项构成,它是一组最小项之和,因此是一个最小项表达式。
对照表2.2.2,上式中各最小项可分别表示为m7、M6、M3、M1,所以可写为
L(A,B,C)=m1+m3+m6+m7。
MB3771PF-G-BND-NH-ER观察表2.2.1可以看出,最小项具有下列性质:
对于任意一个最小项,输人变量只有一组取值使得它的值为1,而在变量取其他各组值时,这个最小项的值都是0。
不同的最小项,使它的值为1的那一组输人变量取值出不同。
对于输入变量的任一组取值,任意两个最小项的乘积为0。
对于输人变量的任一组取值,全体最小项之和为1。
最小项的编号,最小项通常用%表示,下标i即最小项编号,用十进制数表示。将最小项中的原变量用1表示,非变量用0表示,可得到最小项的编号,以ABC为
例,因为它和011相对应的最小项,而011相当于十进制中的3,所以就称ABC记作M3,是和变量取值011相对应的最小项,3,所以把ABC记作m3。按此原则,3个变量的最小项符号如表2.2.2所示。

逻辑函数的最小项表达式,利用逻辑代数的基本公式,可以把任一个逻辑函数化成若干个最小项之和的形式,称为最小项表达式。
例如,逻辑函数L(A,B,C)=AB+AC不是最小项表达式,利用A+A=1的基本运算关系,将逻辑函数中的每一个乘积项都化成包含所有变量A、B、C的项,即
L(A,B,C)=AB+AC=AB(C+C)+AC(B+B)
=ABC+AB C+ACB+AC B
此式由四个最小项构成,它是一组最小项之和,因此是一个最小项表达式。
对照表2.2.2,上式中各最小项可分别表示为m7、M6、M3、M1,所以可写为
L(A,B,C)=m1+m3+m6+m7。
 热门点击
热门点击
- 电压一时间型分段器X、y时限的整定原则
- LA5112N 复杂的数字系统制作
- 馈线自动化的功能与类型
- 7次谐波的实用判据
- MAX6805US44D3+T CMOS集成
- 稳态实验主要是从有无整流负载
- 三电源点的多分段多联络接线故障
- 开闭所DTU与馈线终端FTU的比较
- LM4852LQ MOS管的开关特性
- 对半分割检索算法
 推荐技术资料
推荐技术资料
- 泰克新发布的DSA830
- 泰克新发布的DSA8300在一台仪器中同时实现时域和频域分析,DS... [详细]


 公网安备44030402000607
公网安备44030402000607





