XC9572XL-10VQG44I 二变量卡诺图
发布时间:2019/10/9 21:06:08 访问次数:1650
XC9572XL-10VQG44I这4个方格可以由折叠了的一变量卡诺图展开来获得,例如图2.2.2(a)按箭头方向展开成图2.2.2(b)。在图2.2.2(b)中,变量D标在图的底下,标的规律符合展开的规律[参看图2.2.1(c)],即中间两格底下为D,两边的两格底下为D(图中未标出D)。因为变量C的标法必须区别于D,这样就有两种可能的标法,可以标在展开前两个方格的顶上,也可标在展开后新的两个方格的顶上,图2.2.2(b)采用后一种标法,以保持左边的第一格仍为M0项,即维持展开前两个方格最小项序号不改变。由图2,2.2(b)可看到一个规律:新的方格内最小项的编号比对应的原方格增加了2n~1=22ˉl=2。按照这个规律折叠时[图2.2.2(a)],方格1后面为方格3,方格0后面为方格2,展开后即得图2,2.2(b)所示的二变量卡诺图。
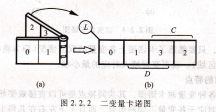
图2,2.2 二变量卡诺图
综上所述,可归纳“折叠展开”的法则如下:
新增加的方格按展开方向应标以新变量。
新的方格内最小项编号应为展开前对应方格编号加2Nˉ1。
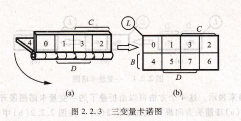
按照同样的方法,可从折叠的二变量卡诺图展开获得三变量卡诺图。三变量逻辑函数乙(C,D,E)应有8个最小项,可用8个相邻的方格来表示,这8个方格可由图2.2.3(a)展开成图2.2.3(b)来获得。新增加的4个方格按展开方向应标以新增加的变量B(以区别于原来的变量C、D)c而且,新增加的方格内最小项的编号为展开前对应方格编号加2刀^1=23^l=4,这样即可获得三变量卡诺图,如图2.2,3(b)所示。在图中,可根据某一方格所处的位置,列出该方格代表的最小项,例如,2号方格处于变量为B、C、D的区域,则m2=BCD,余类推。
XC9572XL-10VQG44I这4个方格可以由折叠了的一变量卡诺图展开来获得,例如图2.2.2(a)按箭头方向展开成图2.2.2(b)。在图2.2.2(b)中,变量D标在图的底下,标的规律符合展开的规律[参看图2.2.1(c)],即中间两格底下为D,两边的两格底下为D(图中未标出D)。因为变量C的标法必须区别于D,这样就有两种可能的标法,可以标在展开前两个方格的顶上,也可标在展开后新的两个方格的顶上,图2.2.2(b)采用后一种标法,以保持左边的第一格仍为M0项,即维持展开前两个方格最小项序号不改变。由图2,2.2(b)可看到一个规律:新的方格内最小项的编号比对应的原方格增加了2n~1=22ˉl=2。按照这个规律折叠时[图2.2.2(a)],方格1后面为方格3,方格0后面为方格2,展开后即得图2,2.2(b)所示的二变量卡诺图。

图2,2.2 二变量卡诺图
综上所述,可归纳“折叠展开”的法则如下:
新增加的方格按展开方向应标以新变量。
新的方格内最小项编号应为展开前对应方格编号加2Nˉ1。
按照同样的方法,可从折叠的二变量卡诺图展开获得三变量卡诺图。三变量逻辑函数乙(C,D,E)应有8个最小项,可用8个相邻的方格来表示,这8个方格可由图2.2.3(a)展开成图2.2.3(b)来获得。新增加的4个方格按展开方向应标以新增加的变量B(以区别于原来的变量C、D)c而且,新增加的方格内最小项的编号为展开前对应方格编号加2刀^1=23^l=4,这样即可获得三变量卡诺图,如图2.2,3(b)所示。在图中,可根据某一方格所处的位置,列出该方格代表的最小项,例如,2号方格处于变量为B、C、D的区域,则m2=BCD,余类推。




 公网安备44030402000607
公网安备44030402000607





