MM1320ANRE 逻辑函数的化简方法
发布时间:2019/10/9 20:32:54 访问次数:991
MM1320ANRE以上五个式子是同一函数不同形式的最简表达式。
逻辑函数化简就是要消去与一或表达式中多余的乘积项和每个乘积项中多余的变量,以得到逻辑函数的最简与一或表达式。有了最简与一或表达式以后,再用公式变换就可以得到其他类型的函数式,所以下面着重讨论与一或表达式的化简。
逻辑函数的化简方法
逻辑函数的化简方法,常用的有代数法和卡诺图法(2.2节介绍)等。代数法就是运用逻辑代数的基本定律和恒等式对逻辑函数进行化简,这种方法需要一些技巧,没有固定的步骤。下面是经常使用的方法:
并项法,利用A+A=1的公式,将两项合并成一项,并消去一个变量。
例2.1.3 试用并项法化简下列与一或逻辑函数表达式。
L1=A BC+ABC
L2=A(BC+BC)+B(BC+BC)
解: (1) L1=AB(C+C)=AB
(2) L2 =ABC+ABC+AB C+A BC
=AB(C+C)+AB(C+C)
=A(B+B)=A
什么是逻辑代数?
求:(1)A+1;(2)A・0;(3)A・A;
写出二变量摩根定理的表达式。
最简与-或表达式的标准是什么?
(4)A+A。
利用代数法可使逻辑函数变成较简单的形式,但经代数法化简后得到的逻辑表达式是否为最简式较难判断。本节介绍的卡诺图①法可以比较简便地得到最简的逻辑表达式。
最小项的意义,N个变量 X1、X2、...xn的最小项是N个因子的乘积,每个变量都以它的原变量或非变量的形式在乘积项中出现,且仅出现一次。
例如,A、B、C3个逻辑变量的最小项有23=8个,即ABC、处BC、AB C、
AB(9、⒕BC、A R9、AB C、ABC, 而AB、ABCA、A(B+C)等则不是最小项。 一般N个变量的最小项应有2个。
最小项的性质,为了分析最小项的性质,下面列出3个变量A、B、C所有最小项的真值表,如表2.2.1所示。
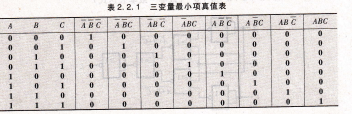
表2,2.1 三变量最小项真值表,逻辑代数与硬件叙述语言基础。
MM1320ANRE以上五个式子是同一函数不同形式的最简表达式。
逻辑函数化简就是要消去与一或表达式中多余的乘积项和每个乘积项中多余的变量,以得到逻辑函数的最简与一或表达式。有了最简与一或表达式以后,再用公式变换就可以得到其他类型的函数式,所以下面着重讨论与一或表达式的化简。
逻辑函数的化简方法
逻辑函数的化简方法,常用的有代数法和卡诺图法(2.2节介绍)等。代数法就是运用逻辑代数的基本定律和恒等式对逻辑函数进行化简,这种方法需要一些技巧,没有固定的步骤。下面是经常使用的方法:
并项法,利用A+A=1的公式,将两项合并成一项,并消去一个变量。
例2.1.3 试用并项法化简下列与一或逻辑函数表达式。
L1=A BC+ABC
L2=A(BC+BC)+B(BC+BC)
解: (1) L1=AB(C+C)=AB
(2) L2 =ABC+ABC+AB C+A BC
=AB(C+C)+AB(C+C)
=A(B+B)=A
什么是逻辑代数?
求:(1)A+1;(2)A・0;(3)A・A;
写出二变量摩根定理的表达式。
最简与-或表达式的标准是什么?
(4)A+A。
利用代数法可使逻辑函数变成较简单的形式,但经代数法化简后得到的逻辑表达式是否为最简式较难判断。本节介绍的卡诺图①法可以比较简便地得到最简的逻辑表达式。
最小项的意义,N个变量 X1、X2、...xn的最小项是N个因子的乘积,每个变量都以它的原变量或非变量的形式在乘积项中出现,且仅出现一次。
例如,A、B、C3个逻辑变量的最小项有23=8个,即ABC、处BC、AB C、
AB(9、⒕BC、A R9、AB C、ABC, 而AB、ABCA、A(B+C)等则不是最小项。 一般N个变量的最小项应有2个。
最小项的性质,为了分析最小项的性质,下面列出3个变量A、B、C所有最小项的真值表,如表2.2.1所示。

表2,2.1 三变量最小项真值表,逻辑代数与硬件叙述语言基础。
 热门点击
热门点击
- 电压一时间型分段器X、y时限的整定原则
- LA5112N 复杂的数字系统制作
- 馈线自动化的功能与类型
- 7次谐波的实用判据
- MAX6805US44D3+T CMOS集成
- 稳态实验主要是从有无整流负载
- 三电源点的多分段多联络接线故障
- 开闭所DTU与馈线终端FTU的比较
- LM4852LQ MOS管的开关特性
- 对半分割检索算法
 推荐技术资料
推荐技术资料
- 泰克新发布的DSA830
- 泰克新发布的DSA8300在一台仪器中同时实现时域和频域分析,DS... [详细]


 公网安备44030402000607
公网安备44030402000607





