MC54HC194J 全定制或半定制的方法
发布时间:2020/2/8 18:19:01 访问次数:908
MC54HC194J权码的十进制数与二进制数之间可用下式来表示
(Ⅳ)D=T-363+W282+W131+WO30 (1.4.1)
式中50~60‰为二进制码中各位的权。
余3码是自补码,与2421码有类似的自补性。余3码也是无权码,它的每1位没有一定的权值,不能用式(1.4.1)来表示其编码关系,但其编码可以由8421码加3(0011)得出。
余3循环码也是一种无权码,它的特点是具有相邻性,任意两个相邻代码之间仅有1位取值不同,例如4和5两个代码0100和1100仅33不同。余3循环码可以看成是将格雷码首尾各3种状态去掉而得到的。下面介绍格雷码。
格雷系Gray的译称,格雷码也是一种常见的无权码,其编码如表1.4.2所示。它也具有相邻性,即两个相邻代码之间仅有1位取值不同,因而常用于将模拟量转换成用连续二进制数序列表示数字量的系统中。当模拟量发生微小变化而引起数字量从1位变化到相邻位时,例如从3到4,格雷码变化是从0010到0110,只有62位从0变成1,其余三位保持不变。如果对于自然二进制码,其变化是从0011到0100,有3位发生变化,如果b2位从0到1变化所需的时间,比1和3。从1变到0的时间长,则在转换过程中,会产生瞬间错误数码0000出现。而格雷码可以避免错误数码的出现。
条件中只要有一个条件得到满足,这件事就会发生。这种关系称为或逻辑。或是指A闭合或B闭合,即任一个条件具各的意思。仿照前述,可以得出用0、1表示的或逻辑真值表,如表1,5.2所示。若用逻辑表达式来描述,则可写为
L=A+B (1.5.2)
式中符号“+”表示A、B或运算,也称为逻辑加。在某些文献中,也有用符号V、∪来表示或运算,能实现或运算的逻辑电路称为或门,其逻辑符号如图1.5.2(b)和图1.5.2(c)所示。图1.5.2(b)所示为矩形符号,图1.5.2(c)所示为特异形符号。
图1.5.2 或逻辑运算状态。若用逻辑表达式来描述,则rb>NC
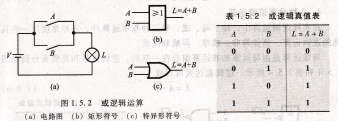
表1.5.2 或逻辑真值表
z=u+f
u=j+k
k的条件为依据。这种逻辑关系称为非逻辑。若用0和1来表示继电器和灯泡的状态,A不通电和灯不亮用0表示,而A通电和灯亮用1表示,则得出非逻辑的真值表,如表1.5.3所示。
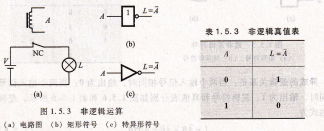
读者很容易看到,b与A总是处于相反的逻辑可写为
L=A (1.5.3)
表1.5.3 非逻辑真值表,二值逻辑变量与基本逻辑运算,(a)电路图 (b)矩形符号 (c)特异形符号.
图1.5.3 非逻辑运算,(a)电路图 (b)矩形符号 (c)特异形符号
深圳市唯有度科技有限公司http://wydkj.51dzw.com/
MC54HC194J权码的十进制数与二进制数之间可用下式来表示
(Ⅳ)D=T-363+W282+W131+WO30 (1.4.1)
式中50~60‰为二进制码中各位的权。
余3码是自补码,与2421码有类似的自补性。余3码也是无权码,它的每1位没有一定的权值,不能用式(1.4.1)来表示其编码关系,但其编码可以由8421码加3(0011)得出。
余3循环码也是一种无权码,它的特点是具有相邻性,任意两个相邻代码之间仅有1位取值不同,例如4和5两个代码0100和1100仅33不同。余3循环码可以看成是将格雷码首尾各3种状态去掉而得到的。下面介绍格雷码。
格雷系Gray的译称,格雷码也是一种常见的无权码,其编码如表1.4.2所示。它也具有相邻性,即两个相邻代码之间仅有1位取值不同,因而常用于将模拟量转换成用连续二进制数序列表示数字量的系统中。当模拟量发生微小变化而引起数字量从1位变化到相邻位时,例如从3到4,格雷码变化是从0010到0110,只有62位从0变成1,其余三位保持不变。如果对于自然二进制码,其变化是从0011到0100,有3位发生变化,如果b2位从0到1变化所需的时间,比1和3。从1变到0的时间长,则在转换过程中,会产生瞬间错误数码0000出现。而格雷码可以避免错误数码的出现。
条件中只要有一个条件得到满足,这件事就会发生。这种关系称为或逻辑。或是指A闭合或B闭合,即任一个条件具各的意思。仿照前述,可以得出用0、1表示的或逻辑真值表,如表1,5.2所示。若用逻辑表达式来描述,则可写为
L=A+B (1.5.2)
式中符号“+”表示A、B或运算,也称为逻辑加。在某些文献中,也有用符号V、∪来表示或运算,能实现或运算的逻辑电路称为或门,其逻辑符号如图1.5.2(b)和图1.5.2(c)所示。图1.5.2(b)所示为矩形符号,图1.5.2(c)所示为特异形符号。
图1.5.2 或逻辑运算状态。若用逻辑表达式来描述,则rb>NC

表1.5.2 或逻辑真值表
z=u+f
u=j+k
k的条件为依据。这种逻辑关系称为非逻辑。若用0和1来表示继电器和灯泡的状态,A不通电和灯不亮用0表示,而A通电和灯亮用1表示,则得出非逻辑的真值表,如表1.5.3所示。

读者很容易看到,b与A总是处于相反的逻辑可写为
L=A (1.5.3)
表1.5.3 非逻辑真值表,二值逻辑变量与基本逻辑运算,(a)电路图 (b)矩形符号 (c)特异形符号.
图1.5.3 非逻辑运算,(a)电路图 (b)矩形符号 (c)特异形符号
深圳市唯有度科技有限公司http://wydkj.51dzw.com/



 公网安备44030402000607
公网安备44030402000607





