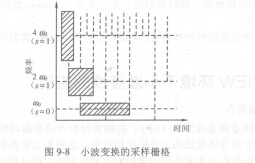
小波变换的采样栅格
发布时间:2014/6/29 13:40:22 访问次数:949
变动基本小波函数中的s和f,可以得NC7S04P5X到一组小波函数。尺度因子s的变动使函数拉伸或压缩,形成不同级的小波。s的增加,将缩小小波的时窗宽度,从而改进小波的时间分辨率,但频率分辨率降低。因此小波分析在高频段有好的时间分辨率,而在低频段有好的频率分辨率。移位系数r的变劫使函数平移,形成不同位的小波,从而反映相应频段信号的时间信息。
图9—8为小波变换的采样栅格。假定基本小波V(t)的中心频率是coo,带宽为如。那么v(2st)的中心频率为2scoo,带宽为2s A∞。对于不同的尺度因子s,虽然时间分辨率和频率分辨率在变,但是带宽和中心频率之比保持一个常数,因此小波分析又叫恒品质因数分析。
尽管小波分析有许多这样引人注目的特点,但它的数学实现却不能像传统的傅里叶变换和短时傅里叶变换那样可以直接做到。首先是基本小波的选择问题。与传统傅里叶变换必须用复正弦函数为基函数不同,小波变换有无限的基本小波可以选择。虽然任意函数都可以用于式(9-2),但是只有能用得到的小波系数恢复原始信号时,V(t)才是有价值的小波。为了重建原来的信号,基本小波的选择不能是任意的,它要受到“容许条件”的限制。因此应用小波变换最大的问题就是选择适当的基本小波V(t)。小波函数生成一直是该领域重要的研究方向之一。其次,在数字信号分析中对尺度因子s常用二进离散,s=2J。不过当待分析的尺度级数较多时,随着.『的增加,vj(n)的点数太多,会给计算造成极大困难。
变动基本小波函数中的s和f,可以得NC7S04P5X到一组小波函数。尺度因子s的变动使函数拉伸或压缩,形成不同级的小波。s的增加,将缩小小波的时窗宽度,从而改进小波的时间分辨率,但频率分辨率降低。因此小波分析在高频段有好的时间分辨率,而在低频段有好的频率分辨率。移位系数r的变劫使函数平移,形成不同位的小波,从而反映相应频段信号的时间信息。
图9—8为小波变换的采样栅格。假定基本小波V(t)的中心频率是coo,带宽为如。那么v(2st)的中心频率为2scoo,带宽为2s A∞。对于不同的尺度因子s,虽然时间分辨率和频率分辨率在变,但是带宽和中心频率之比保持一个常数,因此小波分析又叫恒品质因数分析。

尽管小波分析有许多这样引人注目的特点,但它的数学实现却不能像传统的傅里叶变换和短时傅里叶变换那样可以直接做到。首先是基本小波的选择问题。与传统傅里叶变换必须用复正弦函数为基函数不同,小波变换有无限的基本小波可以选择。虽然任意函数都可以用于式(9-2),但是只有能用得到的小波系数恢复原始信号时,V(t)才是有价值的小波。为了重建原来的信号,基本小波的选择不能是任意的,它要受到“容许条件”的限制。因此应用小波变换最大的问题就是选择适当的基本小波V(t)。小波函数生成一直是该领域重要的研究方向之一。其次,在数字信号分析中对尺度因子s常用二进离散,s=2J。不过当待分析的尺度级数较多时,随着.『的增加,vj(n)的点数太多,会给计算造成极大困难。
上一篇:小波变换简介
上一篇:典型两通道理想重建滤波器组



 公网安备44030402000607
公网安备44030402000607





