从集成电路的输入/输出关系上分析
发布时间:2011/11/9 10:35:54 访问次数:2769
在电路图中,集成电路仅以一个矩形或三角形图框表示,一般不画出内部电路,这给分析电路图带来一定难度。在缺乏集成电路内部电路资料的情况下,如何看懂电路图呢?可以通过分析集成电路输入信号与输出信号的关系看懂整个电路图。
集成电路输出信号与输入信号之间的关系主要有幅度变化关系、频率变化关系、阻抗变化关系、相位变化关系和波形变化关系等。
(1)幅度变化关系
集成电路的输出信号与输入信号相比, JS28F256M29EWH其幅度发生了变化而其他参数不变,如图8-17所示.
如果输出信号的幅度大于输入信号,就可以判定这个集成电路是一个放大电路,如电压放大器、中频放大器、前置放大器、功率放大器等。如果输出信号的幅度小于输入信号,则该集成电路是一个衰减电路,如衰减器、分压器等。

(2)频率变化关系
8成电路的输出信号与输入信号相比,其频率发生了变化,如图8-18所示。
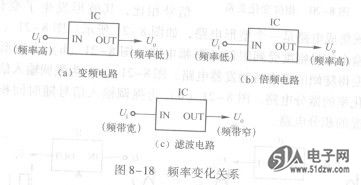
如果输出信号的频率低于输入信号,则该集成电路是一个变频电路。如果输出信号的频率高于输入信号,则该集成电路是一个倍频电路。如果输出信号的频带是输入信号的一部分,则该集成电路是一个滤波电路。
(3)阻抗变化关系
集成电路的输出信号与输入信号相比,其阻抗发生了变化,则该集成电路是一个阻抗变换电路,如图8-19所示。

如果输出信号的阻抗低于输入信号,则该集成电路是电压跟随器、缓冲器等。如果输出信号的阻抗高于输入信号,则该集成电路是阻抗匹配电路、恒流输出电路等。
(4)相位变化关系
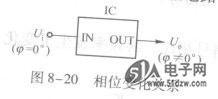
集成电路的输出信号与输入信号相比,其相位发生了变化,则该集成电路是~个移相电路,如图8-20所示。如果移相角度为180。,则可以称为反相电路。
(5)波形变化关系
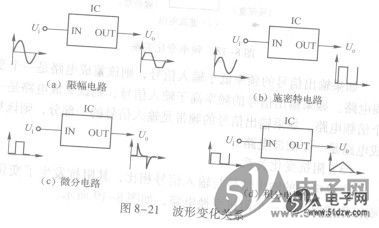
集成电路的输出信号与输入信号相比,其波形发生了变化,则该集成电路是一个整形电路,如图8-21所示。图8-21 (a)为输出信号幅度受到限制的限幅电路。图8-21 (b)为波形边沿变得陡峭的施密特触发器电路。图8-21 (c)为强调输入信号变化率的微分电路。图8-21 (d)为强调输入信号随时间积累情况的积分电路。
除此之外,还有诸如调制关系、解调关系、逻辑关系、控制关系等。有些集成电路的输入/输出信号之间可能同时包含数种上述基本关系,甚至具有更复杂的输入/输出关系。因此,熟练掌握这些基本关系,有助于融会贯通、举一反三地分析各种集成电路电路图。
在电路图中,集成电路仅以一个矩形或三角形图框表示,一般不画出内部电路,这给分析电路图带来一定难度。在缺乏集成电路内部电路资料的情况下,如何看懂电路图呢?可以通过分析集成电路输入信号与输出信号的关系看懂整个电路图。
集成电路输出信号与输入信号之间的关系主要有幅度变化关系、频率变化关系、阻抗变化关系、相位变化关系和波形变化关系等。
(1)幅度变化关系
集成电路的输出信号与输入信号相比, JS28F256M29EWH其幅度发生了变化而其他参数不变,如图8-17所示.
如果输出信号的幅度大于输入信号,就可以判定这个集成电路是一个放大电路,如电压放大器、中频放大器、前置放大器、功率放大器等。如果输出信号的幅度小于输入信号,则该集成电路是一个衰减电路,如衰减器、分压器等。

(2)频率变化关系
8成电路的输出信号与输入信号相比,其频率发生了变化,如图8-18所示。

如果输出信号的频率低于输入信号,则该集成电路是一个变频电路。如果输出信号的频率高于输入信号,则该集成电路是一个倍频电路。如果输出信号的频带是输入信号的一部分,则该集成电路是一个滤波电路。
(3)阻抗变化关系
集成电路的输出信号与输入信号相比,其阻抗发生了变化,则该集成电路是一个阻抗变换电路,如图8-19所示。

如果输出信号的阻抗低于输入信号,则该集成电路是电压跟随器、缓冲器等。如果输出信号的阻抗高于输入信号,则该集成电路是阻抗匹配电路、恒流输出电路等。
(4)相位变化关系
集成电路的输出信号与输入信号相比,其相位发生了变化,则该集成电路是~个移相电路,如图8-20所示。如果移相角度为180。,则可以称为反相电路。

(5)波形变化关系
集成电路的输出信号与输入信号相比,其波形发生了变化,则该集成电路是一个整形电路,如图8-21所示。图8-21 (a)为输出信号幅度受到限制的限幅电路。图8-21 (b)为波形边沿变得陡峭的施密特触发器电路。图8-21 (c)为强调输入信号变化率的微分电路。图8-21 (d)为强调输入信号随时间积累情况的积分电路。

除此之外,还有诸如调制关系、解调关系、逻辑关系、控制关系等。有些集成电路的输入/输出信号之间可能同时包含数种上述基本关系,甚至具有更复杂的输入/输出关系。因此,熟练掌握这些基本关系,有助于融会贯通、举一反三地分析各种集成电路电路图。


 公网安备44030402000607
公网安备44030402000607





