S100114Y 带通滤波电路的通带宽度
发布时间:2020/2/11 20:56:36 访问次数:1237
S100114Y由表9.3.1可找到二阶巴特沃思滤波器的奸F1=1.586,因此,由两级串联的带通滤波电路的通带电压增益(A网)2=(1,586)2≈2,515,由于所需要的通带增益为0 dB,因此在低通滤波器输人部分加了一个由电阻R1、R2组成的分压器。预计图9.3.11所示电路能满足要求。
元件参数的选择和计算,在选用元件时,应当考虑由于元件参数值误差对传递函数存在影响。现规定选择电阻值的容差为1%,电容值的容差为5%。由于每一电路包含若干电阻器和两个电容器,预计实际截止频率可能存在较大的误差(也许是±10%)。为确保在100 Hz和10 kHz处的衰减不大于3 dB。现以额定截止频率90 Hz和11 kHz进行设计。
前已指出,在运放电路中的电阻不宜选择过大或太小。一般为几千欧至几十千欧较合适。因此,选择低通级电路的电容值为1 000 pF,高通级电路的电容值为0.1 uF。然后由式(9.3.5)可计算出精确的电阻值。
对于低通级,由于已知C=1 000 pF和d=11 kHz,由式(9,3.5)算得R3=14.47 kΩ,现选择标准电阻值R3=14,0 kΩ。对于高通级可作同样的计算。由于已知C=0.1 uF和几=90 Hz,可求得R7=R8≈18 kΩ。
考虑到已知Am=1.586,同时尽量要使运放同相输人端和反相输人端对地的直流电阻基本相等,现选择R5=68 kΩ,r6=82 kΩ,由此可算出R4=(uF1-1)R5≈39,8 kΩ,R9=(Am-1)uo≈48 kΩ,其容差为1%。
设计完成的电路如图9.3.11所示。信号源oI通过R1和R2进行衰减,它的戴维宁电阻是Rl和R2的并联值,这个电阻应当等于低通级电阻j=(14 kΩ)。
因此,有u≈R=14 kΩ (⒐3.13)
由于整个滤波电路通带增益是电压分压器比值和滤波器部分增益的乘积,且应等于单位增益,故有
R1r2・(uF)=2.26・2.515=1 (⒐3.14)
联解式(9,3.13)和式(9,3,14),并选择容差为1%的额定电阻值,得Rl=35.7 kΩ和R2=23,2 kΩ。
仿真实验,为确保电路参数满足技术要求,用蒙特卡罗方法①,随机地对图9.3,11电路元件参数选择20组,用SPICE进行仿真,画出例9.3.2带通滤波电路幅
蒙特卡罗系Montc Caio的译称n,高阶有源滤波电路,令s=jω代人式(9.3.17),则有AJωA(jω)=A0(⒐3,18)
1+jo式(9.3.18)表明,当ω=ω0时,图9.3.13所示电路具有最大电压增益,且|A(jω0)|=A0=A vF/(3-A lT),这就是带通滤波电路的通带电压增益。根据式(9.3.18),不难求出其幅频响应,如图9.3.14所示。由图可见,Q值越高,通带越窄。Ro=RV。同相比例图9.3.13 二阶有源带通滤波电路.
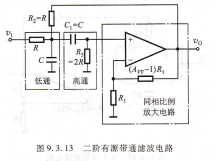
图9.3.14 图9.3,13所示电路的幅频响应,当式(9.3.18)分母虚部的绝对值为1时,有|处(加)|=Ao/√n;因此,利用|O(u~g)|=1,取正根,可求出带通滤波电路的两个截止角频率,从而导出带通滤波电路的通带宽度BW=ω0/(2πO)=yi/Q。
(F-1)Rl=0.5=1
深圳市唯有度科技有限公司http://wydkj.51dzw.com/
S100114Y由表9.3.1可找到二阶巴特沃思滤波器的奸F1=1.586,因此,由两级串联的带通滤波电路的通带电压增益(A网)2=(1,586)2≈2,515,由于所需要的通带增益为0 dB,因此在低通滤波器输人部分加了一个由电阻R1、R2组成的分压器。预计图9.3.11所示电路能满足要求。
元件参数的选择和计算,在选用元件时,应当考虑由于元件参数值误差对传递函数存在影响。现规定选择电阻值的容差为1%,电容值的容差为5%。由于每一电路包含若干电阻器和两个电容器,预计实际截止频率可能存在较大的误差(也许是±10%)。为确保在100 Hz和10 kHz处的衰减不大于3 dB。现以额定截止频率90 Hz和11 kHz进行设计。
前已指出,在运放电路中的电阻不宜选择过大或太小。一般为几千欧至几十千欧较合适。因此,选择低通级电路的电容值为1 000 pF,高通级电路的电容值为0.1 uF。然后由式(9.3.5)可计算出精确的电阻值。
对于低通级,由于已知C=1 000 pF和d=11 kHz,由式(9,3.5)算得R3=14.47 kΩ,现选择标准电阻值R3=14,0 kΩ。对于高通级可作同样的计算。由于已知C=0.1 uF和几=90 Hz,可求得R7=R8≈18 kΩ。
考虑到已知Am=1.586,同时尽量要使运放同相输人端和反相输人端对地的直流电阻基本相等,现选择R5=68 kΩ,r6=82 kΩ,由此可算出R4=(uF1-1)R5≈39,8 kΩ,R9=(Am-1)uo≈48 kΩ,其容差为1%。
设计完成的电路如图9.3.11所示。信号源oI通过R1和R2进行衰减,它的戴维宁电阻是Rl和R2的并联值,这个电阻应当等于低通级电阻j=(14 kΩ)。
因此,有u≈R=14 kΩ (⒐3.13)
由于整个滤波电路通带增益是电压分压器比值和滤波器部分增益的乘积,且应等于单位增益,故有
R1r2・(uF)=2.26・2.515=1 (⒐3.14)
联解式(9,3.13)和式(9,3,14),并选择容差为1%的额定电阻值,得Rl=35.7 kΩ和R2=23,2 kΩ。
仿真实验,为确保电路参数满足技术要求,用蒙特卡罗方法①,随机地对图9.3,11电路元件参数选择20组,用SPICE进行仿真,画出例9.3.2带通滤波电路幅
蒙特卡罗系Montc Caio的译称n,高阶有源滤波电路,令s=jω代人式(9.3.17),则有AJωA(jω)=A0(⒐3,18)
1+jo式(9.3.18)表明,当ω=ω0时,图9.3.13所示电路具有最大电压增益,且|A(jω0)|=A0=A vF/(3-A lT),这就是带通滤波电路的通带电压增益。根据式(9.3.18),不难求出其幅频响应,如图9.3.14所示。由图可见,Q值越高,通带越窄。Ro=RV。同相比例图9.3.13 二阶有源带通滤波电路.

图9.3.14 图9.3,13所示电路的幅频响应,当式(9.3.18)分母虚部的绝对值为1时,有|处(加)|=Ao/√n;因此,利用|O(u~g)|=1,取正根,可求出带通滤波电路的两个截止角频率,从而导出带通滤波电路的通带宽度BW=ω0/(2πO)=yi/Q。
(F-1)Rl=0.5=1

深圳市唯有度科技有限公司http://wydkj.51dzw.com/


 公网安备44030402000607
公网安备44030402000607





