NANOSMDM012-02 数字电路来存储或处理十进制数
发布时间:2019/10/8 12:25:27 访问次数:1571
NANOSMDM012-02人们在日常生活中经常遇到计数问题,并且习惯于用十进制数。而在数字系统,例如计算机中,通常采用二进制数,有时也采用十六进制数或八进制数。这种多位数码的构成方式以及从低位到高位的进位规则称为数制。
众所周知,中国的珠算盘是一个十进制计数器。任何一个数都可以用O、1、2、3、4、5、6、7、8、9等十个数码中的一个或几个,按一定的规律排列起来表示,其计数规律是“逢十进一”,即9+1=10,其中左边的“1”为十位数,右边的“0”为个位数,也就是10=1×10|+0×1o0。所谓十进制就是以10为基数的计数体制。
这样,每一数码处于不同的位置时,它所代表的数值是不同的。例如,十进制数4587.29可以表示为4587.29=4×103+5×102+8×101-卜7×100+2×10ˉ1 +9×10ˉ2式中103、102、101和100分别为千位、百位、十位和个位数码的权,而小数点以右数码的权值是10的负幂。这与珠算盘横梁上所标示的个、十、百、千的位权是相同的。
一般地说,任意十进制数可表示为
(Ⅳ)D①=∑凡×10立 (1・2.1)
式中Ki为基数“10”的第j次幂的系数,它可以是0~9中任何一个数字。
如果将式(1.2.1)中的10用字母R来代替,就可以得到任意进制数的表达式
(Ⅳ)R=∑凡×R氵 (⒈2・2)
式中Kj是第j次幂的系数,根据基数R的不同,它的取值为0~R-1个不同的数码。例如对于十进制数,R为10,所以Ki的取值为0~9共10个数码。
用数字电路来存储或处理十进制数是不方便的。因为构成数字电路的基本思路是把电路的状态与数码对应起来。而十进制的十个数码要求电路有十个完
全不同的状态,这样使得电路很复杂,因此在数字电路中不直接处理十进制数。
二进制的表示方法,二进制数中,只有0和1两个数码,并且计数规律是“逢二进一”,即1+1=10(读为“壹零”)。必须注意,这里的“10”与十进制数的“10”是完
全不同的,它并不代表数“拾”。左边的“1”表示21位数,右边的“0”表示2°位数,也就是10=1×21+0×20。因此,所谓二进制就是以2为基数的计数体制。
根据式(⒈2.2),任意二进制数可表示为
(Ⅳ):②=∑KJ×2. (⒈2.3)
式中Kj为基数“2”的第j次幂的系数,它可以是0或者1。这样式(1.2.3)也可以作为二进制数转换为十进制数的转换公式。
例1,2.1 试将二进制数(1010110):转换为十进制数。
解:将每1位二进制数与其位权相乘,然后相加便得相应的十进制数。
(1010110):=1×26+0×25+1×24+O x23+1×
22+1 ×21 +0 ×20=(86)D
二进制的优点
与十进制相比较,二进制具有一定的优点,因此它在计算机技术中被广泛采用。
二进制的数字装置简单可靠,所用元件少。
二进制只有两个数码0和1,因此它的每1位数都可用任何具有两个不同稳定状态的元件来表示,例如BJT的饱和与截止,继电器接点的闭合和断开,灯泡的亮和不亮等。只要规定其中一种状态表示1,另一种状态表示0,就可以表示二进制数。这样,数码的存储、分析和传输,就可以用简单而可靠的方式进行。
二进制的基本运算规则简单,运算操作方便。
但是,采用二进制也有一些缺点。用二进制表示一个数时,位数多,例如,十进制数49表示为二进制数时,即为110001,使用起来不方便也不习惯。因此,在运算时原始数据多用人们习惯的十进制数,在送入机器时,就必须将十进制原始数据转换成数字系统能接受的二进制数。而在运算结束后,再将二进制数转换为十进制数,表示最终结果。
二进制数的波形表示
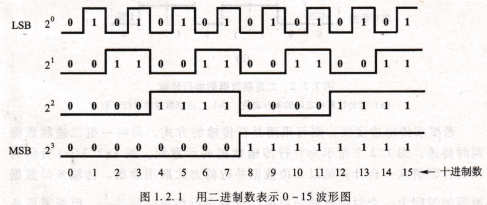
在数字电子技术和计算机应用中,二值数据常用数字波形来表示。这样,数据比较直观,也便于使用电子示波器进行监视。图1.2.1所示为一计数器的波形,图中最左列标出了二进制数的位权(2°、2】、22、23)以及最低位(LSB)①和最高位(MSB)②,最后一行标出了从0到15的等效十进制数。
NANOSMDM012-02人们在日常生活中经常遇到计数问题,并且习惯于用十进制数。而在数字系统,例如计算机中,通常采用二进制数,有时也采用十六进制数或八进制数。这种多位数码的构成方式以及从低位到高位的进位规则称为数制。
众所周知,中国的珠算盘是一个十进制计数器。任何一个数都可以用O、1、2、3、4、5、6、7、8、9等十个数码中的一个或几个,按一定的规律排列起来表示,其计数规律是“逢十进一”,即9+1=10,其中左边的“1”为十位数,右边的“0”为个位数,也就是10=1×10|+0×1o0。所谓十进制就是以10为基数的计数体制。
这样,每一数码处于不同的位置时,它所代表的数值是不同的。例如,十进制数4587.29可以表示为4587.29=4×103+5×102+8×101-卜7×100+2×10ˉ1 +9×10ˉ2式中103、102、101和100分别为千位、百位、十位和个位数码的权,而小数点以右数码的权值是10的负幂。这与珠算盘横梁上所标示的个、十、百、千的位权是相同的。
一般地说,任意十进制数可表示为
(Ⅳ)D①=∑凡×10立 (1・2.1)
式中Ki为基数“10”的第j次幂的系数,它可以是0~9中任何一个数字。
如果将式(1.2.1)中的10用字母R来代替,就可以得到任意进制数的表达式
(Ⅳ)R=∑凡×R氵 (⒈2・2)
式中Kj是第j次幂的系数,根据基数R的不同,它的取值为0~R-1个不同的数码。例如对于十进制数,R为10,所以Ki的取值为0~9共10个数码。
用数字电路来存储或处理十进制数是不方便的。因为构成数字电路的基本思路是把电路的状态与数码对应起来。而十进制的十个数码要求电路有十个完
全不同的状态,这样使得电路很复杂,因此在数字电路中不直接处理十进制数。
二进制的表示方法,二进制数中,只有0和1两个数码,并且计数规律是“逢二进一”,即1+1=10(读为“壹零”)。必须注意,这里的“10”与十进制数的“10”是完
全不同的,它并不代表数“拾”。左边的“1”表示21位数,右边的“0”表示2°位数,也就是10=1×21+0×20。因此,所谓二进制就是以2为基数的计数体制。
根据式(⒈2.2),任意二进制数可表示为
(Ⅳ):②=∑KJ×2. (⒈2.3)
式中Kj为基数“2”的第j次幂的系数,它可以是0或者1。这样式(1.2.3)也可以作为二进制数转换为十进制数的转换公式。
例1,2.1 试将二进制数(1010110):转换为十进制数。
解:将每1位二进制数与其位权相乘,然后相加便得相应的十进制数。
(1010110):=1×26+0×25+1×24+O x23+1×
22+1 ×21 +0 ×20=(86)D
二进制的优点
与十进制相比较,二进制具有一定的优点,因此它在计算机技术中被广泛采用。
二进制的数字装置简单可靠,所用元件少。
二进制只有两个数码0和1,因此它的每1位数都可用任何具有两个不同稳定状态的元件来表示,例如BJT的饱和与截止,继电器接点的闭合和断开,灯泡的亮和不亮等。只要规定其中一种状态表示1,另一种状态表示0,就可以表示二进制数。这样,数码的存储、分析和传输,就可以用简单而可靠的方式进行。
二进制的基本运算规则简单,运算操作方便。
但是,采用二进制也有一些缺点。用二进制表示一个数时,位数多,例如,十进制数49表示为二进制数时,即为110001,使用起来不方便也不习惯。因此,在运算时原始数据多用人们习惯的十进制数,在送入机器时,就必须将十进制原始数据转换成数字系统能接受的二进制数。而在运算结束后,再将二进制数转换为十进制数,表示最终结果。
二进制数的波形表示
在数字电子技术和计算机应用中,二值数据常用数字波形来表示。这样,数据比较直观,也便于使用电子示波器进行监视。图1.2.1所示为一计数器的波形,图中最左列标出了二进制数的位权(2°、2】、22、23)以及最低位(LSB)①和最高位(MSB)②,最后一行标出了从0到15的等效十进制数。



 公网安备44030402000607
公网安备44030402000607





