形状参数m是这三个参数中最重要的一个参数,
发布时间:2015/6/18 21:30:46 访问次数:2051
1.形状参数m
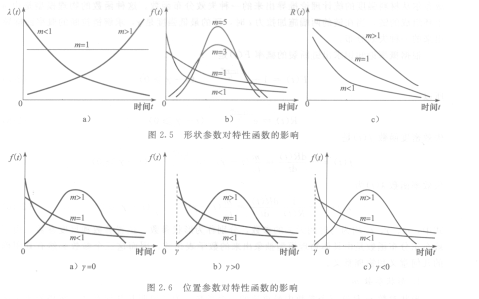
形状参数m是这三个参数中最重要的一个参数,为了说明其几何意义,AT24C1024C1-10CI-2.7将描绘出上述函数图形,分别得到图2.5a、b和c,一O的情况下,m取值不同时,威布尔分布的可靠性函数曲线。从图2.5中可以看出,m值的大小不同,曲线的形状就不同,因此,m值决定了威布尔分布函数曲线的形状,故称为形状参数。从物理本质上看,曲线的不同形状反映出失效分布类型不同,对应于不同的失效物理机制。因此,可以根据m值来确定和判断电子产品的失效类型,受形状参数影响最显著的是失效密度函数曲线,按m<1、m一1、m>1分成三种失效类型。当m>1时,m值越大,曲线峰值越高、越尖锐。
2.位置参数y
为绘图方便,仇为定值,取不同的y值时,绘出失效密度函数,如图2.6所示。由图2.6可以看出,当m、£。相同,不同的y时,其失效密度函数曲线的形状是完全一样的,所不同的只是曲线在时间坐标轴上的位置平行移动,故称y为位置参数。y>O时的曲线,等于由y—O时的曲线向右平行移了距离y;),<0时的曲线,等于由y—o的曲线向左平行移动了距离I yI。从物理本质上来说,位置参数并不改变产品失效分布类型,y<0,表示某些产品从开始工作时就已经有失效品,即这些产品在储存期间(即工作之前)就已经有产品失效;而y>0,表示产品在),时间内,在规定条件下工作,绝对不会出现产品的失效,也就是说,产品存在一个绝对安全期。一般情况下,受试或工作的产品都应是好的,而且要保证产品在特定时间内不出现失效是比较少见的,因此,通常均假设y=0,.这样既比较符合实际情况,又比较方便分析问题。
1.形状参数m
形状参数m是这三个参数中最重要的一个参数,为了说明其几何意义,AT24C1024C1-10CI-2.7将描绘出上述函数图形,分别得到图2.5a、b和c,一O的情况下,m取值不同时,威布尔分布的可靠性函数曲线。从图2.5中可以看出,m值的大小不同,曲线的形状就不同,因此,m值决定了威布尔分布函数曲线的形状,故称为形状参数。从物理本质上看,曲线的不同形状反映出失效分布类型不同,对应于不同的失效物理机制。因此,可以根据m值来确定和判断电子产品的失效类型,受形状参数影响最显著的是失效密度函数曲线,按m<1、m一1、m>1分成三种失效类型。当m>1时,m值越大,曲线峰值越高、越尖锐。
2.位置参数y
为绘图方便,仇为定值,取不同的y值时,绘出失效密度函数,如图2.6所示。由图2.6可以看出,当m、£。相同,不同的y时,其失效密度函数曲线的形状是完全一样的,所不同的只是曲线在时间坐标轴上的位置平行移动,故称y为位置参数。y>O时的曲线,等于由y—O时的曲线向右平行移了距离y;),<0时的曲线,等于由y—o的曲线向左平行移动了距离I yI。从物理本质上来说,位置参数并不改变产品失效分布类型,y<0,表示某些产品从开始工作时就已经有失效品,即这些产品在储存期间(即工作之前)就已经有产品失效;而y>0,表示产品在),时间内,在规定条件下工作,绝对不会出现产品的失效,也就是说,产品存在一个绝对安全期。一般情况下,受试或工作的产品都应是好的,而且要保证产品在特定时间内不出现失效是比较少见的,因此,通常均假设y=0,.这样既比较符合实际情况,又比较方便分析问题。

上一篇:威布尔分布函数



 公网安备44030402000607
公网安备44030402000607





