关联维计算及其简便算法
发布时间:2014/6/29 13:54:09 访问次数:644
分形几何给出了传统的欧氏几何和微积分不能描述的一大类不十分光滑或不规则的集合和函数的一般结构,OM6357EL/3C3/5A作为研究各种复杂现象的一个崭新的方法,近年来在状态识别中得到越来越广泛的应用。振动的时间波形、建筑物原型观测数据等反映被监测对象状态的特征信号,都在一定尺度内具有分形特征。分形理论的主要工具是它形式众多的维数。其中,关联维数对吸引子的不均匀性反应敏感,更能反映吸引子的动态结构。但是从振功加速度
等单变量的时间序列求系统的关联维数通常需要复杂的计算和估计过程,影响状态识别的实时性。因此研究关联维数的简化算法是状态识别技术的迫切需要。随着虚拟仪器在测试技术领域的普及,有越来越多的监测系统建立在以LabVIEW为代表的虚拟仪器平台上,优化计算关联维的LabVIEW程序具有重要的工程实际意义。
由时间序列重构相空间
在状态识别工程实际中,一般只能得到系统一个状态变量的输出,例如水坝体径向位移、机械设备振动加速度等。这些直接测量到的时间序列是系统中各种要素综合作用的结果,包含系统的动力特性,因此需要从这个时间序列抽取动力系统,重构成高维的相空间。重构相空间通常采用时延法,设系统的嵌入维数为m,延迟时间,构造出状态空间中的向量。
墨对应m维相空间中的一个点,Ⅳ个点构成相空间中一条动力学轨道。
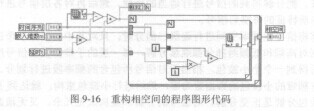
LabVIEW开发环境中提供的大量数组函数为构造相空间提供了极大的便利。图9-16是构造相空间的程序图形代码。图中内层的For循环构造相空间中的一个点;外层的For循环构造完整的相空间:For循环外面的代码计算Ⅳ。
分形几何给出了传统的欧氏几何和微积分不能描述的一大类不十分光滑或不规则的集合和函数的一般结构,OM6357EL/3C3/5A作为研究各种复杂现象的一个崭新的方法,近年来在状态识别中得到越来越广泛的应用。振动的时间波形、建筑物原型观测数据等反映被监测对象状态的特征信号,都在一定尺度内具有分形特征。分形理论的主要工具是它形式众多的维数。其中,关联维数对吸引子的不均匀性反应敏感,更能反映吸引子的动态结构。但是从振功加速度
等单变量的时间序列求系统的关联维数通常需要复杂的计算和估计过程,影响状态识别的实时性。因此研究关联维数的简化算法是状态识别技术的迫切需要。随着虚拟仪器在测试技术领域的普及,有越来越多的监测系统建立在以LabVIEW为代表的虚拟仪器平台上,优化计算关联维的LabVIEW程序具有重要的工程实际意义。
由时间序列重构相空间
在状态识别工程实际中,一般只能得到系统一个状态变量的输出,例如水坝体径向位移、机械设备振动加速度等。这些直接测量到的时间序列是系统中各种要素综合作用的结果,包含系统的动力特性,因此需要从这个时间序列抽取动力系统,重构成高维的相空间。重构相空间通常采用时延法,设系统的嵌入维数为m,延迟时间,构造出状态空间中的向量。
墨对应m维相空间中的一个点,Ⅳ个点构成相空间中一条动力学轨道。
LabVIEW开发环境中提供的大量数组函数为构造相空间提供了极大的便利。图9-16是构造相空间的程序图形代码。图中内层的For循环构造相空间中的一个点;外层的For循环构造完整的相空间:For循环外面的代码计算Ⅳ。

上一篇:采样信号中噪声的影响与抑制
上一篇:相空间中欧氏距离的简化计算



 公网安备44030402000607
公网安备44030402000607





