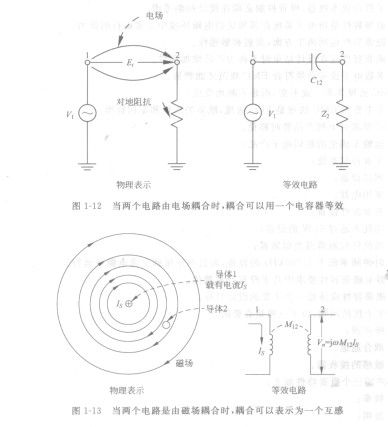
当两个电路由电场耦合时,耦合可以用一个电容器等效
发布时间:2014/4/7 16:06:38 访问次数:912
为了准确回答一个电路是如何工作的,必须求EPM7032LC44-15解麦克斯韦方程组。这些方程是三个空间变量(x,y,z)和时间(t)的函数——一个四维问题。但任何最简单的问题的解通常也是复杂的。为了避免这种复杂性,一种称为“电路分析”的近似分析技术被用在大多数设计过程中。
电路分析消去了空间的变量,提供了只有时间(或频率)变量的函数的近似解。假设如下:
(1)所有的电场被限制在电容器的内部。
(2)所有的磁场被限制在电感器的内部。
(3)电路尺寸小于讨论的波长。
真正隐含的外场,即使实际存在,在网络解决方案中可以被忽略。然而,对其他电路的影响,这些外场不一定可以被忽略。
例如,一个100W的功率放大器可以辐射lOOmW的功率。就功率放大器的分析和运行而言,这lOOmW的功率完全可以忽略不计。但是,如果这辐射功率的一小部分被一个敏感电路的输入端接收,就可能造成干扰。
尽管对100W功率放大器来说,lOOmW辐射发射完全可以忽略不计,但是在合适的条件下,一个敏感的无线电接收机,可能接收到几千英里以外的信号。
只要有可能,噪声耦合通道表示为等效集总元件网络。例如,存在于两个导体之间的时变电场,可以用连接在两个导体之间的电容器表示,如图1-12所示。两个导体之间耦合的时变磁场可以用两个电路之间的互感表示,如图1-13所示。
为了准确回答一个电路是如何工作的,必须求EPM7032LC44-15解麦克斯韦方程组。这些方程是三个空间变量(x,y,z)和时间(t)的函数——一个四维问题。但任何最简单的问题的解通常也是复杂的。为了避免这种复杂性,一种称为“电路分析”的近似分析技术被用在大多数设计过程中。
电路分析消去了空间的变量,提供了只有时间(或频率)变量的函数的近似解。假设如下:
(1)所有的电场被限制在电容器的内部。
(2)所有的磁场被限制在电感器的内部。
(3)电路尺寸小于讨论的波长。
真正隐含的外场,即使实际存在,在网络解决方案中可以被忽略。然而,对其他电路的影响,这些外场不一定可以被忽略。
例如,一个100W的功率放大器可以辐射lOOmW的功率。就功率放大器的分析和运行而言,这lOOmW的功率完全可以忽略不计。但是,如果这辐射功率的一小部分被一个敏感电路的输入端接收,就可能造成干扰。
尽管对100W功率放大器来说,lOOmW辐射发射完全可以忽略不计,但是在合适的条件下,一个敏感的无线电接收机,可能接收到几千英里以外的信号。
只要有可能,噪声耦合通道表示为等效集总元件网络。例如,存在于两个导体之间的时变电场,可以用连接在两个导体之间的电容器表示,如图1-12所示。两个导体之间耦合的时变磁场可以用两个电路之间的互感表示,如图1-13所示。




 公网安备44030402000607
公网安备44030402000607





