正态性检验
发布时间:2012/10/21 16:04:32 访问次数:1385
正态性检验可用概率密度函IRFHM9331TRPBF数分析、卡埃平方拟合优度检验法、偏态峰态检验法。平稳随机振动数据的概率结构非常重要。一般假设随机信号服从正态(或高斯)分布,它的概率密度函数为
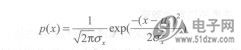
其中,以和Ux分别为信号的均值和标准偏差。当产生信号的结构单元或气动噪声单元中包含有非线性特征时,随机信号的概率分布与正态性有明显的差别,可能会直接影响到对信号的解释和应用。这种可能性可以通过该信号的概率密度函数计算,并将它与上式所给的正态概率密度函数相比较来评定。也可用正态性检验。
有几种不同的正态性统计检验方法,最广泛采用的是Z2拟合良好性检验。当统计独立的数据值茌200~2 000个之间时,Z2检验最有效。由于动态数据的离散时间序列值通常都是与时间相关的,根据经验,这种检验方法适用于100< BT<1 000的离散时间序列,其中B为主要动态数据值的近似频带宽,而丁为数据序列的持续时间。
当对随机信号进行概率密度分析或拟合良好性检验时,要求信号必须是平稳的。如果信号是非平稳的,特别是有时变的标准偏差时,即使产生测量结果的现象本身确实是服从高斯分布的,但根据时间平均计算得到的概率密度函数会呈现非高斯分布。因此,重要的是,概率密度计算和正态性检验的前提是要求测量数据是平稳的,否则会产生虚假的正态性偏差。
正态性检验可用概率密度函IRFHM9331TRPBF数分析、卡埃平方拟合优度检验法、偏态峰态检验法。平稳随机振动数据的概率结构非常重要。一般假设随机信号服从正态(或高斯)分布,它的概率密度函数为
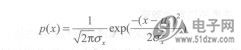
其中,以和Ux分别为信号的均值和标准偏差。当产生信号的结构单元或气动噪声单元中包含有非线性特征时,随机信号的概率分布与正态性有明显的差别,可能会直接影响到对信号的解释和应用。这种可能性可以通过该信号的概率密度函数计算,并将它与上式所给的正态概率密度函数相比较来评定。也可用正态性检验。
有几种不同的正态性统计检验方法,最广泛采用的是Z2拟合良好性检验。当统计独立的数据值茌200~2 000个之间时,Z2检验最有效。由于动态数据的离散时间序列值通常都是与时间相关的,根据经验,这种检验方法适用于100< BT<1 000的离散时间序列,其中B为主要动态数据值的近似频带宽,而丁为数据序列的持续时间。
当对随机信号进行概率密度分析或拟合良好性检验时,要求信号必须是平稳的。如果信号是非平稳的,特别是有时变的标准偏差时,即使产生测量结果的现象本身确实是服从高斯分布的,但根据时间平均计算得到的概率密度函数会呈现非高斯分布。因此,重要的是,概率密度计算和正态性检验的前提是要求测量数据是平稳的,否则会产生虚假的正态性偏差。



 公网安备44030402000607
公网安备44030402000607





