临界频率
发布时间:2012/7/3 20:01:45 访问次数:2182
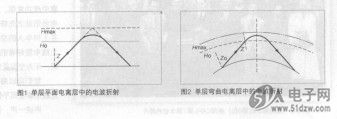
我们从单层的平面电GRM155C1H271JA01D离层开始,其峰值处具有最大电子浓度Nmax,其高度为离地球表面Hmax,如图1所示。这种模型可以用于显示晚上的状态,当E层的电离降到一个低水平而仅剩下了F2层。我们知道,从发射机垂直向上发出,并能作为回波返回地面的最高频率,称为该层的临界频率㈣,Filfc=(9E-6)×SQRT㈨给出,其中为高度在的电子浓度。
当一个发射机以高于地平线的一个角度发送射频电波,或者说以与垂直或天顶方向的夹角Z发射。射频电波以角度Z进入电离层的底部,然后因为折射而产生一个弯曲的传播路径。这种情况下,对于斜入射,从该层(电离)峰值处回到地面的最高频率理论上要比fe大1/cosZ倍。举个例子,假设fe等于4MHz而角度2等于60。。这时,电子浓度Nmay为2E+11/m3,丽以这个入射角返回的。频率为8.OMHz,是垂直入射临界频率的两倍。
这个简单的例子显示了短波传播是如何工作的。一个8.OMHz的信号以斜入射而回到地面,其路径的偏转要更小一些(60。),而不是垂直入射时4MHz信号的180。。这个结果产生的原因是,较高频率的信号沿着斜路径上遇到的电子数量比垂直入射的临界频率信号遇到的要大得多。
因此,短波通信在远低于临界频率(用电离层探测来获得)的频率上传播也是可能的,其极限由头顶上的电子浓度和天线的辐射方向图所决定。当然,更低的频率∽也可以沿着斜入射角传播,只是它们无法在电离层中穿透得更远。由于频率为fmax的辐射由frnax=fc/cosZ给出,它以与天顶夹角为Z的角度传播,并到达高度为P0。的电离层顶部,而此处的电子浓度为Nmax,那么它的等效垂直频率就为COL70以此而言,较低频率∞的辐射会有一个较低的等效垂直频率,×COt7,会在一个较低的高度返回,该高度上的电子浓度N可以根据等式f×cos2=(9E一6)×SClRT(N)得到,而实际高度可从电子浓度剖面得到。
除了这个重要结论之外,图1还显示了以一个入射角进入电寓层时的地面范围,或称跳跃距离。图1指出了射频被向下折射时的实际高度,以及射频如同被一个电离层“镜子”反射回来时的虚拟高度之间的差别。
尽管镜面反射这个想法在传播的讨论中还是有作用的,但必须记住,它是象征性的,而不是实际发生的情况。究其原因,一面镜子当然没有折射特性,因而无法表示电离层的这一主要特征,即传播路径会跟随频率变化而改变。处理电离层问题更好的方法,无论折射还是反射,是要将地球的曲率包括进来,用球面几何来计算路径的详情,用6378km代表地球的半径。除了在高度Ho时的入射角Z,弯曲的电离层是从Ho处开始的,还要将球面几何的问题考虑进去。在图2所示的几何图形中,在高度Ho处的天项角Z是与射频从地面发射处的天顶角不一样的(更小)。
除了这项调整以外,还有一个修正系数(k)必须加到1/cos2因子中,这是因为电离层本身的弯曲效应。修正系数就变成了k/cosZ,其中k随着距离而线性地变化,由lOCOkm路径的1.05到3000km路径的大约1 20。随着这些变化,你就可以对最大频率frnax做出很好的估算,它是被弯曲电离层送回地面的,该电离层具有临界频率饩)和在高度Hax处达到峰值的电子浓度剖面。
我们从单层的平面电GRM155C1H271JA01D离层开始,其峰值处具有最大电子浓度Nmax,其高度为离地球表面Hmax,如图1所示。这种模型可以用于显示晚上的状态,当E层的电离降到一个低水平而仅剩下了F2层。我们知道,从发射机垂直向上发出,并能作为回波返回地面的最高频率,称为该层的临界频率㈣,Filfc=(9E-6)×SQRT㈨给出,其中为高度在的电子浓度。
当一个发射机以高于地平线的一个角度发送射频电波,或者说以与垂直或天顶方向的夹角Z发射。射频电波以角度Z进入电离层的底部,然后因为折射而产生一个弯曲的传播路径。这种情况下,对于斜入射,从该层(电离)峰值处回到地面的最高频率理论上要比fe大1/cosZ倍。举个例子,假设fe等于4MHz而角度2等于60。。这时,电子浓度Nmay为2E+11/m3,丽以这个入射角返回的。频率为8.OMHz,是垂直入射临界频率的两倍。
这个简单的例子显示了短波传播是如何工作的。一个8.OMHz的信号以斜入射而回到地面,其路径的偏转要更小一些(60。),而不是垂直入射时4MHz信号的180。。这个结果产生的原因是,较高频率的信号沿着斜路径上遇到的电子数量比垂直入射的临界频率信号遇到的要大得多。

因此,短波通信在远低于临界频率(用电离层探测来获得)的频率上传播也是可能的,其极限由头顶上的电子浓度和天线的辐射方向图所决定。当然,更低的频率∽也可以沿着斜入射角传播,只是它们无法在电离层中穿透得更远。由于频率为fmax的辐射由frnax=fc/cosZ给出,它以与天顶夹角为Z的角度传播,并到达高度为P0。的电离层顶部,而此处的电子浓度为Nmax,那么它的等效垂直频率就为COL70以此而言,较低频率∞的辐射会有一个较低的等效垂直频率,×COt7,会在一个较低的高度返回,该高度上的电子浓度N可以根据等式f×cos2=(9E一6)×SClRT(N)得到,而实际高度可从电子浓度剖面得到。
除了这个重要结论之外,图1还显示了以一个入射角进入电寓层时的地面范围,或称跳跃距离。图1指出了射频被向下折射时的实际高度,以及射频如同被一个电离层“镜子”反射回来时的虚拟高度之间的差别。
尽管镜面反射这个想法在传播的讨论中还是有作用的,但必须记住,它是象征性的,而不是实际发生的情况。究其原因,一面镜子当然没有折射特性,因而无法表示电离层的这一主要特征,即传播路径会跟随频率变化而改变。处理电离层问题更好的方法,无论折射还是反射,是要将地球的曲率包括进来,用球面几何来计算路径的详情,用6378km代表地球的半径。除了在高度Ho时的入射角Z,弯曲的电离层是从Ho处开始的,还要将球面几何的问题考虑进去。在图2所示的几何图形中,在高度Ho处的天项角Z是与射频从地面发射处的天顶角不一样的(更小)。
除了这项调整以外,还有一个修正系数(k)必须加到1/cos2因子中,这是因为电离层本身的弯曲效应。修正系数就变成了k/cosZ,其中k随着距离而线性地变化,由lOCOkm路径的1.05到3000km路径的大约1 20。随着这些变化,你就可以对最大频率frnax做出很好的估算,它是被弯曲电离层送回地面的,该电离层具有临界频率饩)和在高度Hax处达到峰值的电子浓度剖面。
 热门点击
热门点击


 公网安备44030402000607
公网安备44030402000607





