振幅频率特性
发布时间:2012/5/10 20:22:10 访问次数:1719
在图3.9中,表示图3.1电路的STM32F207ZGT6电压增益、相位与频率(lkHz~lOMHz)的曲线图。
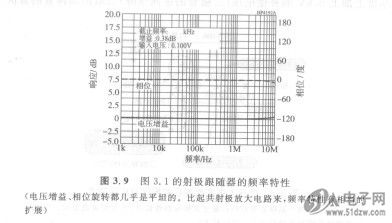
在电压增益为OdB( =1)、相位为O。(输入输出同相位)处,特性为直线几乎延伸至10MHz。在10MHz附近,增益的上升认为是由于测量仪器与电路的高频失配引起的。
如图3.10所示,射极跟随器的频率特性也与共射极电路的情况一样,基极串联电阻rs与电路的输入电容Ci形成的低通滤波器使得高频增益下降。
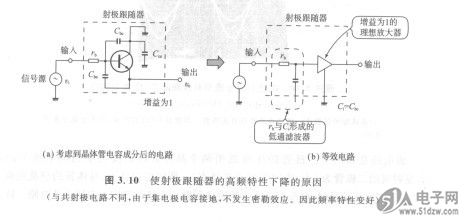
但是,射极跟随器的增益仅为1,所以不发生密勒效应,因此非常小,如图3.9所示,频率特性变得非常好。
在图3.11中,表示低频的频率特性。低频截止频率约为3.3Hz,与用前面的式(3.3)计算得到的在输入侧形成的高通滤波器的截止频率(3.2Hz)几乎一致。在图3.11的测量中,没有接负载,因此在曲线中没有出现C2与负载所形成的高通滤波器的特性。

在图3.9中,表示图3.1电路的STM32F207ZGT6电压增益、相位与频率(lkHz~lOMHz)的曲线图。

在电压增益为OdB( =1)、相位为O。(输入输出同相位)处,特性为直线几乎延伸至10MHz。在10MHz附近,增益的上升认为是由于测量仪器与电路的高频失配引起的。
如图3.10所示,射极跟随器的频率特性也与共射极电路的情况一样,基极串联电阻rs与电路的输入电容Ci形成的低通滤波器使得高频增益下降。

但是,射极跟随器的增益仅为1,所以不发生密勒效应,因此非常小,如图3.9所示,频率特性变得非常好。
在图3.11中,表示低频的频率特性。低频截止频率约为3.3Hz,与用前面的式(3.3)计算得到的在输入侧形成的高通滤波器的截止频率(3.2Hz)几乎一致。在图3.11的测量中,没有接负载,因此在曲线中没有出现C2与负载所形成的高通滤波器的特性。

上一篇:改进后的推挽型射极跟随器
上一篇:噪声及总谐波失真率


 公网安备44030402000607
公网安备44030402000607





