MIC298182YWMTR不对称的双凸形翼型
发布时间:2019/11/10 22:06:13 访问次数:2412
MIC298182YWMTR能不变这样在流动中只有压力能和动能之间的相互转换。压力能是由于流体有压力而具各的做功能力,单位体积流体所具有的压力能用压力P来表示。动能是由于流体有速度而具备的做功能力,单位体积流体所具有的动能用告1/2pu2来表示。这样,伯努利方程数学表达式可写成:
p+1/2pu2=po=常数 (2-4)
式中:p――静压。单位体积流体具有的压力能。在静止的空气中,静压等于大气压力。
2pu――动压。单位体积流体具有的动能。其中p是空气的密度,u是流体的运动速度。
pO――总压。静压和动压之和。
式(2-4)是不可压缩、理想流体作定常流动时的伯努利方程。
将式(2-3)的连续方程和式(2-4)伯努利方程一起考虑,可以得出以下结论:不可压缩的、理想的流体在进行定常流动时,流管变细,流线变密,流体的流速将增加,流体的动压增大,静压将减小;反之,流管变粗,流线变疏,流体的流速将减小,流体的动压减小,静压将增加。
图2-5所示的实验可以定性地说明这个结果。当管道中的空气静止时,管道中各处的大气压力都一样,都等于此处的大气压力,所以,各测压管中指示剂液面的高度都相等,如图2-5(a)所示。但当空气以某一速度连续稳定地流过管道时,情况就发生了变化,困为流动管道内的空气压力都有所下降,所以各测压管中指示剂的液面都有所升高,但升高的量却不一样。管截面最细处的液面升高量最大,而管截面最粗处的液面升高量最小,如图2-5(b)所示。这就是在忽略了空气可压缩性的情况下,空气连续而稳定的流过管道,在管截面最细处的速度最快,空气的压力下降的最多;在管截面最粗处的速度最慢,空气的压力下降的最小的原因所致。
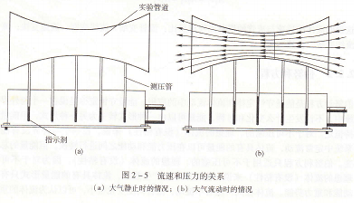
图2-5 流速和压力的关系,(a)大气静止时的情况;(b)大气流动时的情况
通过图2-5所示实验可以说明飞机机翼气动升力的产生。当气流流过机翼表面时,由于气流的方向和机翼所采用的翼型,在机翼表面形成的流管就像图2-5中所示的那样变细或变粗,流体中的压力能和动能之间发生转变,在机翼表面形成不同的压力分布,从而产生升力。这点我们还要在下面进行详细的讲述。
枕体几何外形和参数,机翼的几何外形和参数
机翼的几何外形包括机翼翼型、机翼平面形状和机翼相对机身的安装位置。
机翼翼型,机翼横切面的形状称为机翼翼型。对平直机翼就是用平行机身对称面的平面切割机翼所得机翼的切面形状(见图2-6)。
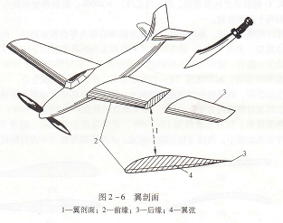
图2-6 翼剖面
1一翼剖面;2一前缘;3一后缘;4一翼弦
表示机翼翼型的参数有:弦线、弦长:翼型最前端的一点叫机翼前缘,最后端的一点叫机翼后缘。连接机翼前缘和机翼后缘的线叫弦线,也叫翼弦。弦线的长度叫几何弦长,简称弦长。用符号3表示(见图2-7)。
厚度、相对厚度:翼弦垂直线与翼型上下翼面的交点之间距离称为翼型的度。
厚度的最大值称为最大厚度εmax。最大厚度与弦长之比C=(Cmax/b) ×100%称为相对厚度。相对厚度的大小表示翼型的厚薄程度,相对厚度大,表示翼型厚;相对厚度小,表示翼型薄。最大厚度的位置可以用最大厚度距前缘的距离Xc和弦长之比来表示。
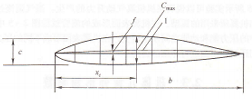
图2-7 翼剖面的特性参数
1一中线;Cmax一翼剖面最大厚度;δ一翼弦长度;f=弯度
Xc=(Xc/b) ×100%。翼型相对厚度和最大厚度的位置是描写翼型的两个重要参数。
中弧线(中线)、弯度、相对弯度:垂直弦线的直线在上下翼面所截线段中点的连线叫中弧线。中弧线到弦线之间的最大距离叫最大弯度,用丸x表示。最大弯度与弦长之比叫相对弯度,f=(fmax/b)×I00%。相对弯度的大小表示翼型的弯曲程度,相对弯度大,表示翼型弯曲程度大;相对弯度小,表示翼型弯曲程度小。最大弯度的位置也用最大弯度距前缘的距离焉和弦长之比来表示。Xf=(Xf/b) ×100%。翼型弯度和最大弯度的位置也是描写翼型的两个重要参数。
翼型可以用弯度特征、厚度特征、前缘半经和后缘角等参数来描述,改变这些参数可以得到不同的翼型(见图2-8)。低亚音速飞机机翼采用的翼型如图2-8(e)所示,它是前缘圆、后缘尖,具有一定弯度的不对称的双凸形翼型,相对厚度约为12%~18%,最大厚度的位置为⒛%左右。对称翼型(g)的弯度为零,中弧线与弦线重合,一般用于尾翼。随着飞行速度的提高,翼型的相对厚度逐渐减小,最大厚度的位置逐渐向后移。目前民用运输机机翼翼型的相对厚度约为8%~I6%,最大厚度的位置约为5%~~sO%。低速飞机机翼采用的翼型弯度较大,相对弯度约为4%~6%,最大弯度位置靠前。随着飞行速度的提高,翼型的弯度也逐渐减小,高速飞机为减小阻力,大多采用弯度为零的对称翼型(j)。
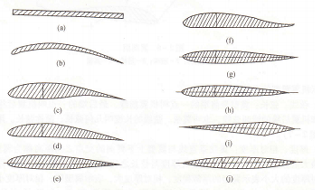
图2-8 各种不同的翼剖面
MIC298182YWMTR能不变这样在流动中只有压力能和动能之间的相互转换。压力能是由于流体有压力而具各的做功能力,单位体积流体所具有的压力能用压力P来表示。动能是由于流体有速度而具备的做功能力,单位体积流体所具有的动能用告1/2pu2来表示。这样,伯努利方程数学表达式可写成:
p+1/2pu2=po=常数 (2-4)
式中:p――静压。单位体积流体具有的压力能。在静止的空气中,静压等于大气压力。
2pu――动压。单位体积流体具有的动能。其中p是空气的密度,u是流体的运动速度。
pO――总压。静压和动压之和。
式(2-4)是不可压缩、理想流体作定常流动时的伯努利方程。
将式(2-3)的连续方程和式(2-4)伯努利方程一起考虑,可以得出以下结论:不可压缩的、理想的流体在进行定常流动时,流管变细,流线变密,流体的流速将增加,流体的动压增大,静压将减小;反之,流管变粗,流线变疏,流体的流速将减小,流体的动压减小,静压将增加。
图2-5所示的实验可以定性地说明这个结果。当管道中的空气静止时,管道中各处的大气压力都一样,都等于此处的大气压力,所以,各测压管中指示剂液面的高度都相等,如图2-5(a)所示。但当空气以某一速度连续稳定地流过管道时,情况就发生了变化,困为流动管道内的空气压力都有所下降,所以各测压管中指示剂的液面都有所升高,但升高的量却不一样。管截面最细处的液面升高量最大,而管截面最粗处的液面升高量最小,如图2-5(b)所示。这就是在忽略了空气可压缩性的情况下,空气连续而稳定的流过管道,在管截面最细处的速度最快,空气的压力下降的最多;在管截面最粗处的速度最慢,空气的压力下降的最小的原因所致。

图2-5 流速和压力的关系,(a)大气静止时的情况;(b)大气流动时的情况
通过图2-5所示实验可以说明飞机机翼气动升力的产生。当气流流过机翼表面时,由于气流的方向和机翼所采用的翼型,在机翼表面形成的流管就像图2-5中所示的那样变细或变粗,流体中的压力能和动能之间发生转变,在机翼表面形成不同的压力分布,从而产生升力。这点我们还要在下面进行详细的讲述。
枕体几何外形和参数,机翼的几何外形和参数
机翼的几何外形包括机翼翼型、机翼平面形状和机翼相对机身的安装位置。
机翼翼型,机翼横切面的形状称为机翼翼型。对平直机翼就是用平行机身对称面的平面切割机翼所得机翼的切面形状(见图2-6)。

图2-6 翼剖面
1一翼剖面;2一前缘;3一后缘;4一翼弦
表示机翼翼型的参数有:弦线、弦长:翼型最前端的一点叫机翼前缘,最后端的一点叫机翼后缘。连接机翼前缘和机翼后缘的线叫弦线,也叫翼弦。弦线的长度叫几何弦长,简称弦长。用符号3表示(见图2-7)。
厚度、相对厚度:翼弦垂直线与翼型上下翼面的交点之间距离称为翼型的度。
厚度的最大值称为最大厚度εmax。最大厚度与弦长之比C=(Cmax/b) ×100%称为相对厚度。相对厚度的大小表示翼型的厚薄程度,相对厚度大,表示翼型厚;相对厚度小,表示翼型薄。最大厚度的位置可以用最大厚度距前缘的距离Xc和弦长之比来表示。

图2-7 翼剖面的特性参数
1一中线;Cmax一翼剖面最大厚度;δ一翼弦长度;f=弯度
Xc=(Xc/b) ×100%。翼型相对厚度和最大厚度的位置是描写翼型的两个重要参数。
中弧线(中线)、弯度、相对弯度:垂直弦线的直线在上下翼面所截线段中点的连线叫中弧线。中弧线到弦线之间的最大距离叫最大弯度,用丸x表示。最大弯度与弦长之比叫相对弯度,f=(fmax/b)×I00%。相对弯度的大小表示翼型的弯曲程度,相对弯度大,表示翼型弯曲程度大;相对弯度小,表示翼型弯曲程度小。最大弯度的位置也用最大弯度距前缘的距离焉和弦长之比来表示。Xf=(Xf/b) ×100%。翼型弯度和最大弯度的位置也是描写翼型的两个重要参数。
翼型可以用弯度特征、厚度特征、前缘半经和后缘角等参数来描述,改变这些参数可以得到不同的翼型(见图2-8)。低亚音速飞机机翼采用的翼型如图2-8(e)所示,它是前缘圆、后缘尖,具有一定弯度的不对称的双凸形翼型,相对厚度约为12%~18%,最大厚度的位置为⒛%左右。对称翼型(g)的弯度为零,中弧线与弦线重合,一般用于尾翼。随着飞行速度的提高,翼型的相对厚度逐渐减小,最大厚度的位置逐渐向后移。目前民用运输机机翼翼型的相对厚度约为8%~I6%,最大厚度的位置约为5%~~sO%。低速飞机机翼采用的翼型弯度较大,相对弯度约为4%~6%,最大弯度位置靠前。随着飞行速度的提高,翼型的弯度也逐渐减小,高速飞机为减小阻力,大多采用弯度为零的对称翼型(j)。

图2-8 各种不同的翼剖面
上一篇:MC92R01平均空气动力弦长



 公网安备44030402000607
公网安备44030402000607





