NCP1012APL130R曲线的切线方向
发布时间:2019/11/10 21:53:45 访问次数:1871
NCP1012APL130R相对运动原理,作用在飞机上的空气动力取决于飞机和空气之间的相对运动情况,而与观察、研究时所选用的参考坐标无关。也就是说,飞机以速度u在平静的空气中飞行时,作用在飞机上的空气动力与远方空气以速度v流过静止不动的飞机时所产生的空气动力完全相同。这就是相对运动原理在空气动力学中的应用。
空气相对飞机的运动称为相对气流,相对气流的方向与飞机运动的方向相反(见图2-1)。只要相对气流速度相同,产生的空气动力也就相等。将飞机的飞行转换为空气的流动,使空气动力问题的研究大大简化。风洞实验就是根据这个原理建立起来的。
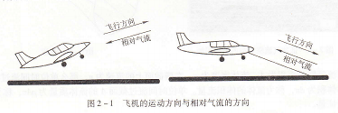
图2-1 飞机的运动方向与相对气流的方向
连续性假设是在进行空气动力学研究时,将大量的、单个分子组成的大气看成是连续的介质。所谓连续介质就是组成介质的物质连成一片,内部没有任何空隙。在其中任意取一个微团都可以看成是由无数分子组成,微团表现出来的特性体现了众多分子的共同特性。对大气采用连续性假设的理由是与所研究的对象――飞机相比,空气分子的平均自由行程要比飞机的尺寸小得多。空气流过飞机表面时,与飞机之间产生的相互作用不是单个分子所为,而是无数分子共同作用的结果。
流场、定常流和非定常流,流体流动所占据的空间称为流场。在流场中的任何一点处,如果流体微团流过时的流动参数――速度、压力、温度、密度等随时间变化,这种流动就称为非定常流,这种流场被称为非定常流场。反之,如果流体微团流过时的流动参数――速度、压力、温度、密度等不随时间变化,这种流动就称为定常流,这种流场被称为定常流场。
流线、流线谱、流管和流量,流线是在流场中用来描绘流体微团流动状态的曲线。在流线每一点上,曲线的切线方向正是流体微团流过该点时流动速度的方向。在流场中,用流线组成的描绘流体微团流动情况的图画称为流线谱。图2-2所示为描绘气流流过翼型的流线谱。如果流线谱不随时间变化,它所描绘的就是定常流。
在流场中取一条不是流线的封闭曲线,通过曲线上各点的流线形成的管形曲面称为流管,如图2-3所示。因为通过曲线上各点流体微团的速度都与通过该点的流线相切,所以只有流管截面上有流体流过,而不会有流体通过管壁流进或流出。
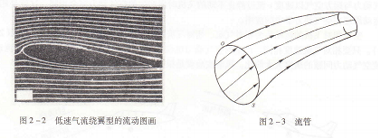
图2-2 低速气流绕翼型的流动图画
若流管横截面积为a,流体密度为ρ,在横截面上的流速为v,那么单位时间流过截面a的流体体积为av,称为流体的体积流量。单位时间流过截面姓的流体质量为pau,称为流体的质量流量。
qm=pAv (2-1)
式中:gm――质量流量,单位kg/s。
流体流动的基本规律
连续方程是质量守恒定律在流体定常流动中的应用。图2-4所示为远方气流以速度v绕流过机翼翼型的定常流线谱,选中一根流管和三个横截面1、2、3。由式(2-1)可知:流体流过三个横截面的质量流量分别等于qm1=ρlA1v1,qm2=p2a2u2,qm3=p3a3u3。流管性质决定了流管内的流体不能穿越管壁流到管外,流管外的流体也不能穿越管壁流到管内,根据质量守恒定律(质量不会自生也不会自灭),可以得出qm1=qm2=qm3.

图2-4 绕翼型的流线谱
连续方程可以表述为:在定常流动中,流体连续并稳定的在流管中流动,通过流管各截面的质量流量相等。即:
ρ1a1u1=ρ2A2u2=ρ3a3u3=・・・ (2-2)
式中:ρ1、p2、p3…----流体流过各截面时的密度;
v1、u2、u3…----流体流过各截面时的速度;
a1、a2、a3…――流管各截面的面积。
对于不可压缩流体,比如,低速飞行时(ma<0.4),可以把大气看成是不可压缩的流体,即密度ρ等于常数,连续方程可以简化为:
A1v1=a2v2=A3v3=… (2-3)
这说明流体的流速与流管的横截面积成反比:流管变细,流线变密,流速变快;流管变粗,流线变疏,流速变慢。
伯努利方程是能量守恒定律在流体流动中的应用。能量守恒定律是说在一个与外界隔绝的系统中,不论发生什么变化和过程,能量可以由一种形式转变为另一种形式,但能量的总和保持恒定。对于不可压缩的、理想的流体(没有粘性)来说,在一个与外界没有能量交换的系统中定常流动,流体具有的能量可以在压力能和动能之间进行转换,但能量的总和保持不变。伯努利方程只适用于不可压缩的、理想的流体(没有粘性)。因为对于不可压缩的、理想的流体(没有粘性)来说,流动中不会产生热量,流体具有的能量形式只有压力能、动能和重力势能。流体在同一流管中流动,流管高度变化很小,可以认为流体的重力势控制体Ω.
NCP1012APL130R相对运动原理,作用在飞机上的空气动力取决于飞机和空气之间的相对运动情况,而与观察、研究时所选用的参考坐标无关。也就是说,飞机以速度u在平静的空气中飞行时,作用在飞机上的空气动力与远方空气以速度v流过静止不动的飞机时所产生的空气动力完全相同。这就是相对运动原理在空气动力学中的应用。
空气相对飞机的运动称为相对气流,相对气流的方向与飞机运动的方向相反(见图2-1)。只要相对气流速度相同,产生的空气动力也就相等。将飞机的飞行转换为空气的流动,使空气动力问题的研究大大简化。风洞实验就是根据这个原理建立起来的。

图2-1 飞机的运动方向与相对气流的方向
连续性假设是在进行空气动力学研究时,将大量的、单个分子组成的大气看成是连续的介质。所谓连续介质就是组成介质的物质连成一片,内部没有任何空隙。在其中任意取一个微团都可以看成是由无数分子组成,微团表现出来的特性体现了众多分子的共同特性。对大气采用连续性假设的理由是与所研究的对象――飞机相比,空气分子的平均自由行程要比飞机的尺寸小得多。空气流过飞机表面时,与飞机之间产生的相互作用不是单个分子所为,而是无数分子共同作用的结果。
流场、定常流和非定常流,流体流动所占据的空间称为流场。在流场中的任何一点处,如果流体微团流过时的流动参数――速度、压力、温度、密度等随时间变化,这种流动就称为非定常流,这种流场被称为非定常流场。反之,如果流体微团流过时的流动参数――速度、压力、温度、密度等不随时间变化,这种流动就称为定常流,这种流场被称为定常流场。
流线、流线谱、流管和流量,流线是在流场中用来描绘流体微团流动状态的曲线。在流线每一点上,曲线的切线方向正是流体微团流过该点时流动速度的方向。在流场中,用流线组成的描绘流体微团流动情况的图画称为流线谱。图2-2所示为描绘气流流过翼型的流线谱。如果流线谱不随时间变化,它所描绘的就是定常流。
在流场中取一条不是流线的封闭曲线,通过曲线上各点的流线形成的管形曲面称为流管,如图2-3所示。因为通过曲线上各点流体微团的速度都与通过该点的流线相切,所以只有流管截面上有流体流过,而不会有流体通过管壁流进或流出。

图2-2 低速气流绕翼型的流动图画
若流管横截面积为a,流体密度为ρ,在横截面上的流速为v,那么单位时间流过截面a的流体体积为av,称为流体的体积流量。单位时间流过截面姓的流体质量为pau,称为流体的质量流量。
qm=pAv (2-1)
式中:gm――质量流量,单位kg/s。
流体流动的基本规律
连续方程是质量守恒定律在流体定常流动中的应用。图2-4所示为远方气流以速度v绕流过机翼翼型的定常流线谱,选中一根流管和三个横截面1、2、3。由式(2-1)可知:流体流过三个横截面的质量流量分别等于qm1=ρlA1v1,qm2=p2a2u2,qm3=p3a3u3。流管性质决定了流管内的流体不能穿越管壁流到管外,流管外的流体也不能穿越管壁流到管内,根据质量守恒定律(质量不会自生也不会自灭),可以得出qm1=qm2=qm3.

图2-4 绕翼型的流线谱
连续方程可以表述为:在定常流动中,流体连续并稳定的在流管中流动,通过流管各截面的质量流量相等。即:
ρ1a1u1=ρ2A2u2=ρ3a3u3=・・・ (2-2)
式中:ρ1、p2、p3…----流体流过各截面时的密度;
v1、u2、u3…----流体流过各截面时的速度;
a1、a2、a3…――流管各截面的面积。
对于不可压缩流体,比如,低速飞行时(ma<0.4),可以把大气看成是不可压缩的流体,即密度ρ等于常数,连续方程可以简化为:
A1v1=a2v2=A3v3=… (2-3)
这说明流体的流速与流管的横截面积成反比:流管变细,流线变密,流速变快;流管变粗,流线变疏,流速变慢。
伯努利方程是能量守恒定律在流体流动中的应用。能量守恒定律是说在一个与外界隔绝的系统中,不论发生什么变化和过程,能量可以由一种形式转变为另一种形式,但能量的总和保持恒定。对于不可压缩的、理想的流体(没有粘性)来说,在一个与外界没有能量交换的系统中定常流动,流体具有的能量可以在压力能和动能之间进行转换,但能量的总和保持不变。伯努利方程只适用于不可压缩的、理想的流体(没有粘性)。因为对于不可压缩的、理想的流体(没有粘性)来说,流动中不会产生热量,流体具有的能量形式只有压力能、动能和重力势能。流体在同一流管中流动,流管高度变化很小,可以认为流体的重力势控制体Ω.



 公网安备44030402000607
公网安备44030402000607





