TK11128CSIL方波信号的时域
发布时间:2019/10/30 13:04:21 访问次数:1848
TK11128CSIL对模拟电子电路进行测试。
由高等数学知识可知,任意周期函数只要满足狄利克雷条件都可以展开成傅里叶级数。对于图1.2.2的周期性方波信号,它的时间函数表达式为
v(t)=vs 当nt≤t<(2t+1)t/2时
v(t)=0 当(2n+1)t/2≤t((n+1)t时 (1.2.2)
式中vs为方波幅值,t为周期,n为从--∞到+∞的整数。
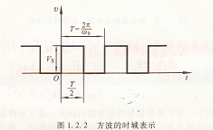
图1.2.2和式(1.2.2)中的电压v是时间t的函数,所以称为方波信号的时域表达方式。
此方波信号可展开为傅里叶级数表达式
u(t)=vs/2+2vs/t(sinω0t+1/3sin3ωot+1/5sin5ωt+…) (⒈⒉3)
式中ωo=2t/t,vs/2是方波信号的直流分量,2vs/tsinω0t为该方波信号的基波,它
的周期钎与方波本身的周期相同。式(1.2.3)中其余各项都是高次谐波分量,它们的角频率是基波角频率的整数倍。根据三角函数知识,由式(1.2.3)可以得到如下形式:
v(t)=vs/2+2vs/t[cos(ω0t-t/2)+1/5cos(5ω0t-t/2)+...] (1.2.4)
即 V(t)=vs/2+2vs/t n=1,3,5... 1/ncos(nω0t-t/2) (1.2.5)
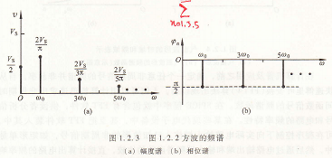
由此可以得到幅值与角频率的关系为如图1.2.3所示的图解形式,其中包括直流项(ω=0)和每一谐波分量在相应角频率处的振幅和相位。这种信号各频率分量的振幅随角频率变化的分布,称为该信号的幅度频谱(简称幅度谱,如图1.2.3a所示);而信号各频率分量的相位随角频率变化的分布,称为该信号的相位频谱(简称相位谱,如图1.2.3b所示),图1.2.3称为该方波信号的频谱图,是其频域表达方式。对于正弦波,其频谱只在基波频率上有相应的幅值,其他频率上的分量全部为零。
从傅里叶级数特性可知,许多周期信号的频谱都由直流分量、基波分量以及无穷多项高次谐波分量所组成,频谱表现为一系列离散频率上的幅值,且随着谐波次数的递增,v(ω)的幅值总趋势是逐渐减小的。如果只截取Ⅳω0(Ⅳ为有限正值)以下的信号组合,则可以得到原周期信号的近似波形,Ⅳ愈大,波形的误差愈小。周期性方波信号亦可作为电子系统的测试信号,例如,当测试宽频带放大器的频率响应时,固然可以采用扫频仪来实现,但当采用方波信号进行测试时,由被测系统输出方波电压的前沿上升是否陡峭和平顶降落的程度,来定性地评价放大器的频带宽度。这是因为方波信号的前沿变化较快,反映高频分量,而平顶部分变化较慢,反映低频分量。详见第4章4~8节。
上述正弦信号和方波信号都是周期信号,在一个周期内已包含了信号的全部信息,任何重复周期都没有新的信息出现。客观物理世界的信号远没有这么简单,如果从时间函数来看,往往很难直螯弭一个简单的表达式来描述,例如气温变化曲线可能如图1.2.4a所示,它就是一非周期性时间函数波形。运用傅里叶变换可将非周期信号表达为一连续频率函数形式的频谱,它包含了所有可能的频率(0≤ω<∞)成分。图1.2,4b示意出图a的频谱函数。实际物理世界的各种非周期信号,随角频率上升到一定程度,其频谱函数总趋势是衰减的。当选择适当的ωc(截止角频率),把高于此频率的部分截断时,不致太多地影响信号的特性。通常把保留的部分称为信号的带宽。
由上分析可知,信号的频域表达方式可以得到某些比时域表达方式更有意义的参数。信号的频谱特性是电子系统有关频率特性的主要设计依据。
TK11128CSIL对模拟电子电路进行测试。
由高等数学知识可知,任意周期函数只要满足狄利克雷条件都可以展开成傅里叶级数。对于图1.2.2的周期性方波信号,它的时间函数表达式为
v(t)=vs 当nt≤t<(2t+1)t/2时
v(t)=0 当(2n+1)t/2≤t((n+1)t时 (1.2.2)
式中vs为方波幅值,t为周期,n为从--∞到+∞的整数。

图1.2.2和式(1.2.2)中的电压v是时间t的函数,所以称为方波信号的时域表达方式。
此方波信号可展开为傅里叶级数表达式
u(t)=vs/2+2vs/t(sinω0t+1/3sin3ωot+1/5sin5ωt+…) (⒈⒉3)
式中ωo=2t/t,vs/2是方波信号的直流分量,2vs/tsinω0t为该方波信号的基波,它
的周期钎与方波本身的周期相同。式(1.2.3)中其余各项都是高次谐波分量,它们的角频率是基波角频率的整数倍。根据三角函数知识,由式(1.2.3)可以得到如下形式:
v(t)=vs/2+2vs/t[cos(ω0t-t/2)+1/5cos(5ω0t-t/2)+...] (1.2.4)
即 V(t)=vs/2+2vs/t n=1,3,5... 1/ncos(nω0t-t/2) (1.2.5)
由此可以得到幅值与角频率的关系为如图1.2.3所示的图解形式,其中包括直流项(ω=0)和每一谐波分量在相应角频率处的振幅和相位。这种信号各频率分量的振幅随角频率变化的分布,称为该信号的幅度频谱(简称幅度谱,如图1.2.3a所示);而信号各频率分量的相位随角频率变化的分布,称为该信号的相位频谱(简称相位谱,如图1.2.3b所示),图1.2.3称为该方波信号的频谱图,是其频域表达方式。对于正弦波,其频谱只在基波频率上有相应的幅值,其他频率上的分量全部为零。
从傅里叶级数特性可知,许多周期信号的频谱都由直流分量、基波分量以及无穷多项高次谐波分量所组成,频谱表现为一系列离散频率上的幅值,且随着谐波次数的递增,v(ω)的幅值总趋势是逐渐减小的。如果只截取Ⅳω0(Ⅳ为有限正值)以下的信号组合,则可以得到原周期信号的近似波形,Ⅳ愈大,波形的误差愈小。周期性方波信号亦可作为电子系统的测试信号,例如,当测试宽频带放大器的频率响应时,固然可以采用扫频仪来实现,但当采用方波信号进行测试时,由被测系统输出方波电压的前沿上升是否陡峭和平顶降落的程度,来定性地评价放大器的频带宽度。这是因为方波信号的前沿变化较快,反映高频分量,而平顶部分变化较慢,反映低频分量。详见第4章4~8节。
上述正弦信号和方波信号都是周期信号,在一个周期内已包含了信号的全部信息,任何重复周期都没有新的信息出现。客观物理世界的信号远没有这么简单,如果从时间函数来看,往往很难直螯弭一个简单的表达式来描述,例如气温变化曲线可能如图1.2.4a所示,它就是一非周期性时间函数波形。运用傅里叶变换可将非周期信号表达为一连续频率函数形式的频谱,它包含了所有可能的频率(0≤ω<∞)成分。图1.2,4b示意出图a的频谱函数。实际物理世界的各种非周期信号,随角频率上升到一定程度,其频谱函数总趋势是衰减的。当选择适当的ωc(截止角频率),把高于此频率的部分截断时,不致太多地影响信号的特性。通常把保留的部分称为信号的带宽。
由上分析可知,信号的频域表达方式可以得到某些比时域表达方式更有意义的参数。信号的频谱特性是电子系统有关频率特性的主要设计依据。




 公网安备44030402000607
公网安备44030402000607





