JRW044V(TE1)电路的完全状态表
发布时间:2019/10/17 21:46:13 访问次数:1097
JRW044V(TE1)所示的电路,这段时间大约在40ns左右。
逻辑功能分析,由状态图和时序图可知,该电路是一个异步二进制减计数器,z信号的上升沿可触发借位操作。也可把它看作为一个序列信号发生器。输出序列脉冲信号z的重复周期为4rcP,脉宽约为1rcP。
例6,4,2 分析图6,4,4所示逻辑电路。
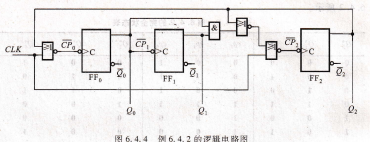
图6.4.4 例6.42的逻辑电路图
解:这是由3个下降沿触发的r′触发器构成的异步时序电路G只要相应触发器的时钟输人端CP。出现一次从1到0的跳变,其状态就会翻转一次。下面按步骤进行分析。
列出各逻辑方程组
根据逻辑图列出各触发器时钟信号的逻辑表达式
CPO=Q2+C乙Κ=Q2C乙K (6・4.3)
CP1=0。 (6.4,4)
CP2=QOO1+Q2+Cz’Κ=(Q001+Q2)C乙~K (6.4.5)
输出方程组
即三个触发器的输出信号o2、Q1、Q0。
状态方程组
引人cp″后,r′触发器的特性方程Q:亠l=0:应改写为如下状态方程
0;tl=口lr``()+0l币T (6・4・6)
0∷1=0{rP】+Ol币「 (⒍4.7)
0∶+l=口:rP2+Q:币・I (⒍4.8)
注意:此例中每当CP″发生由1到0的跳变时印″=1。
列出状态表,从现态o2=o1=G=0开始列状态表。应从C芭Κ所能触发的第一个触发器FF。开始推导其次态。首先确定印0:根据式(⒍4.3),由于Q2=0,C乙Κ信
号0→1的跳变必然使CPO产生一个1→0的跳变,所以cpO=1。然后将cP0和现态Ol=0代人式(6.4.6),得到0:+l=1。类似地,根据式(6.4.5),由于O2=Ql=00=0 i CP2为0,此时CLK的任何变化都不会使CP2产生下降沿,故cp2=0,FF2不会改变状态,o:+l=0。这时9再根据式(6.4.4)确定吼:因为00是0→1跳变,所以cpl=0,Q1也将保持原状。CLK信号第一个上升沿到来后,电路状态改变为001。依此类推,可得电路的完全状态表,如表6.4.2所示。

JRW044V(TE1)所示的电路,这段时间大约在40ns左右。
逻辑功能分析,由状态图和时序图可知,该电路是一个异步二进制减计数器,z信号的上升沿可触发借位操作。也可把它看作为一个序列信号发生器。输出序列脉冲信号z的重复周期为4rcP,脉宽约为1rcP。
例6,4,2 分析图6,4,4所示逻辑电路。

图6.4.4 例6.42的逻辑电路图
解:这是由3个下降沿触发的r′触发器构成的异步时序电路G只要相应触发器的时钟输人端CP。出现一次从1到0的跳变,其状态就会翻转一次。下面按步骤进行分析。
列出各逻辑方程组
根据逻辑图列出各触发器时钟信号的逻辑表达式
CPO=Q2+C乙Κ=Q2C乙K (6・4.3)
CP1=0。 (6.4,4)
CP2=QOO1+Q2+Cz’Κ=(Q001+Q2)C乙~K (6.4.5)
输出方程组
即三个触发器的输出信号o2、Q1、Q0。
状态方程组
引人cp″后,r′触发器的特性方程Q:亠l=0:应改写为如下状态方程
0;tl=口lr``()+0l币T (6・4・6)
0∷1=0{rP】+Ol币「 (⒍4.7)
0∶+l=口:rP2+Q:币・I (⒍4.8)
注意:此例中每当CP″发生由1到0的跳变时印″=1。
列出状态表,从现态o2=o1=G=0开始列状态表。应从C芭Κ所能触发的第一个触发器FF。开始推导其次态。首先确定印0:根据式(⒍4.3),由于Q2=0,C乙Κ信
号0→1的跳变必然使CPO产生一个1→0的跳变,所以cpO=1。然后将cP0和现态Ol=0代人式(6.4.6),得到0:+l=1。类似地,根据式(6.4.5),由于O2=Ql=00=0 i CP2为0,此时CLK的任何变化都不会使CP2产生下降沿,故cp2=0,FF2不会改变状态,o:+l=0。这时9再根据式(6.4.4)确定吼:因为00是0→1跳变,所以cpl=0,Q1也将保持原状。CLK信号第一个上升沿到来后,电路状态改变为001。依此类推,可得电路的完全状态表,如表6.4.2所示。




 公网安备44030402000607
公网安备44030402000607





