EPF10K20TC144-4N二阶有源低通滤波电路
发布时间:2019/11/11 17:50:10 访问次数:1034
EPF10K20TC144-4N二阶有源低通滤波电路①,二阶有源低通滤波电路如图9.3.1所示。由图可见,它是由两节RC滤波电路和同相比例放大电路组成,其特点是输人阻抗高,输出阻抗低。
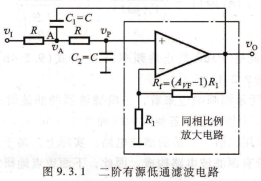
同相比例二阶有源低通滤波电路
前已指出,同相比例放大电路的电压增益就是低通滤波器的通带电压增益, 即AO =Avf =1+(AvF-1)R1/R1。
传递函数,考虑到集成运放的同相输人端电压为
vp(s)=vo(s)/avf (⒐3.1)
而vp(s)与va(s)的关系为
vp(s)=va(s)/1+src (⒐3.2)
对于节点A,应用KCL可得
vi(s)-va(s)-va(s)/r-[va(s)-vo(s)]sc-va(s)-vp(s)/r=0 (⒐3.3)
将式(9.3.1)~(9.3.3)联立求解,可得电路的传递函数为
a(s)=vo(s)/vi(s)
=avf/1+(3-avf)scr+(scr)2 (9,3.4)
图9.3.1在电路发展史上,称为Sallen-Key电路,因为这二位作者于1955年在IRE汇刊上发表了下面的论文: R.P.Sallen and E.L,Key, “A Pracllcal Method of Designing RC Active Filters,” IRE Transations on Circuit Theo0,, ⅤoI CT-2, 74~85, March 1955。
令 ωc=1/rc
Q=1/3-avf
则有 a(s)=avfwc2/s2+wc/qs+wc2
式(9,3.7)为二阶低通滤波电路传递函数的典型表达式。其中ωc=1/(RC)为特征角频率,也是3 dB截止角频率,而Q则称为等效品质因数。式(9.3.4)表明,AO=Avf<3,才能稳定工作。当A0=A,F≥3时,电路将自激振荡。
幅频响应,用s=jω代人式(9.3.7),可得幅频响应和相频响应表达式,分别为
201g|a(jw)/ao|=201g1/[1-(w/wc)2+(w/wcq)2 (⒐3.8)
ω=-arctanw/(wcq)/1-(w/wc)2 (⒐3.9)
式(⒐3,8)表明,当ω=0时,|A(jω)|=avT=Ao;当ω→∞时,|A(jω)|→0。显然,这是低通滤波电路的特性。由式(9.3.8)可画出不同q值下的幅频响应,如图9.3.2所示。由图可见,当Q=0.707时,幅频响应较平坦。当o=0.707和ω/ωc=1情况下,201g|A(jω)/A。|=-3 dB;而当ω/ωc=10时,201g|A(jω)用0|=-40 dB。这表明二阶比一阶低通滤波电路的滤波效果好得多。当进一步增加滤波电路阶数,其幅频响应就更接近理想特性。

n阶巴特沃思传递函数①
如果将图9.3,1的低通滤波电路选取不同的R、C值可得到不同的频率响应曲线,这种工程上使用的滤波器称为巴特沃思、切比雪夫和贝塞尔滤波器。工程上常用查表式软件计算来确定参数。
n阶巴特沃思低通滤波器的传递函数为
|A(jω)|=ao/1+(W/WC)2N (9.3.10)
式中N为滤波电路阶数,ωc为3dB截止角频率,A0为通带电压增益。
由式(9,3.10)可画出其归一化幅频响应曲线如图9.3.3所示。由图可见,随着阶数N增加,其幅频特性将向理想特性逼近。

71阶巴特沃思低通滤波器归一化幅频响应,试用集成运放设计一截止频率五=100Hz的四阶低通巴特沃思滤波器。要求:选择运放;选择和计算全部电阻、电容参数;用SPICE仿真画出幅频响应波特图;用SPICE仿真画出各级和总的归一化幅度响应曲线。
解:由两个二阶低通滤波电路级联而成的四阶低通巴特沃思滤波电路如图9.3.4所示。设计时一般应考虑:对所用运放的技术参数应有适当要求(如增益带宽积、输入阻抗、转换速率等);所选元件数较少,且数值不宜太分析.见本节附录:巴特沃思传递函数。
深圳市唯有度科技有限公司http://wydkj.51dzw.com/
EPF10K20TC144-4N二阶有源低通滤波电路①,二阶有源低通滤波电路如图9.3.1所示。由图可见,它是由两节RC滤波电路和同相比例放大电路组成,其特点是输人阻抗高,输出阻抗低。

同相比例二阶有源低通滤波电路
前已指出,同相比例放大电路的电压增益就是低通滤波器的通带电压增益, 即AO =Avf =1+(AvF-1)R1/R1。
传递函数,考虑到集成运放的同相输人端电压为
vp(s)=vo(s)/avf (⒐3.1)
而vp(s)与va(s)的关系为
vp(s)=va(s)/1+src (⒐3.2)
对于节点A,应用KCL可得
vi(s)-va(s)-va(s)/r-[va(s)-vo(s)]sc-va(s)-vp(s)/r=0 (⒐3.3)
将式(9.3.1)~(9.3.3)联立求解,可得电路的传递函数为
a(s)=vo(s)/vi(s)
=avf/1+(3-avf)scr+(scr)2 (9,3.4)
图9.3.1在电路发展史上,称为Sallen-Key电路,因为这二位作者于1955年在IRE汇刊上发表了下面的论文: R.P.Sallen and E.L,Key, “A Pracllcal Method of Designing RC Active Filters,” IRE Transations on Circuit Theo0,, ⅤoI CT-2, 74~85, March 1955。
令 ωc=1/rc
Q=1/3-avf
则有 a(s)=avfwc2/s2+wc/qs+wc2
式(9,3.7)为二阶低通滤波电路传递函数的典型表达式。其中ωc=1/(RC)为特征角频率,也是3 dB截止角频率,而Q则称为等效品质因数。式(9.3.4)表明,AO=Avf<3,才能稳定工作。当A0=A,F≥3时,电路将自激振荡。
幅频响应,用s=jω代人式(9.3.7),可得幅频响应和相频响应表达式,分别为
201g|a(jw)/ao|=201g1/[1-(w/wc)2+(w/wcq)2 (⒐3.8)
ω=-arctanw/(wcq)/1-(w/wc)2 (⒐3.9)
式(⒐3,8)表明,当ω=0时,|A(jω)|=avT=Ao;当ω→∞时,|A(jω)|→0。显然,这是低通滤波电路的特性。由式(9.3.8)可画出不同q值下的幅频响应,如图9.3.2所示。由图可见,当Q=0.707时,幅频响应较平坦。当o=0.707和ω/ωc=1情况下,201g|A(jω)/A。|=-3 dB;而当ω/ωc=10时,201g|A(jω)用0|=-40 dB。这表明二阶比一阶低通滤波电路的滤波效果好得多。当进一步增加滤波电路阶数,其幅频响应就更接近理想特性。

n阶巴特沃思传递函数①
如果将图9.3,1的低通滤波电路选取不同的R、C值可得到不同的频率响应曲线,这种工程上使用的滤波器称为巴特沃思、切比雪夫和贝塞尔滤波器。工程上常用查表式软件计算来确定参数。
n阶巴特沃思低通滤波器的传递函数为
|A(jω)|=ao/1+(W/WC)2N (9.3.10)
式中N为滤波电路阶数,ωc为3dB截止角频率,A0为通带电压增益。
由式(9,3.10)可画出其归一化幅频响应曲线如图9.3.3所示。由图可见,随着阶数N增加,其幅频特性将向理想特性逼近。

71阶巴特沃思低通滤波器归一化幅频响应,试用集成运放设计一截止频率五=100Hz的四阶低通巴特沃思滤波器。要求:选择运放;选择和计算全部电阻、电容参数;用SPICE仿真画出幅频响应波特图;用SPICE仿真画出各级和总的归一化幅度响应曲线。
解:由两个二阶低通滤波电路级联而成的四阶低通巴特沃思滤波电路如图9.3.4所示。设计时一般应考虑:对所用运放的技术参数应有适当要求(如增益带宽积、输入阻抗、转换速率等);所选元件数较少,且数值不宜太分析.见本节附录:巴特沃思传递函数。
深圳市唯有度科技有限公司http://wydkj.51dzw.com/



 公网安备44030402000607
公网安备44030402000607





