VI-21W-EY 数字密码锁
发布时间:2019/10/25 17:36:09 访问次数:2332
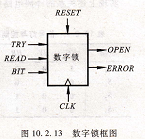
VI-21W-EY数字密码锁内部由8个拨动开关设置了8位二进制密码,分别用D7、D6、D5、D4、D3、D2、D1、DO表示。开锁时的串行输人数码由BFr开关产生,可以为0或1,如图10.2.13所示,为了使系统REr能1位1位地依次读取由Brr开关送来的串行数码,设置了1个按钮开关RmD,送入数码 my时,首先用Brr开关设置1位数码,然后按下RE'DRE4D开关,这样就将Brr开关产生的当前数Brr码读入系统。为了标识串行数码输入开始和结束,设置了RESEr和「Ry按钮开关,RESEr
信号使系统进入初始状态,准备接受新的串行数码,当送8位数码与开锁密码一致时,按下图10.2.13 数字锁框图rRy产生开锁信号,系统便输出0PEⅣ信号打开锁,否则数字锁不开,并输出错误信号ERROR。
将系统划分为控制单元和处理单元,将数字密码锁划分为控制单元和处理单元两部分如图10.2.14所示,控制单元控制处理单元接受Brr产生的数码,并将其与对应的密码位相比较,比较结果召作为状态信息送到控制单元。为累计输人数码的位数,需要一个计数器。控制单元发出的控制信号C乙R使计数器清零,并使数码的比较从低位开利用A+AB=A的公式,消去多余的项AB。根据代入规则,A、B可以是任何一个复杂的逻辑式。
例2.1.4 试用吸收法化简逻辑函数表达式山=处B+ABCDE+ABCDF。
解: u=AB+ABCI9(E+F)=AB
消去法,利用A+AB=⒕+B,消去多余的因子。
例2.1.5 试用消去法化简逻辑函数表达式乙=AB+AC+BC。
解: u=AB+(A+B)C
=AB+aBC
=AB+C
配项法,先利用A=△(B+B),增加必要的乘积项,再用并项或吸收的办法使项数
减少。
例2,1.6 试用配项法化简逻辑函数表达式L=AB+AC+BC。
解: u=AB+AC+(A+A)BC
=AB+AC+AB C+AB C
=(AB+AB C)+(AC+AC)B)
=AB+AC
使用配项的方法要有一定的经验,否则越配越繁。通常对逻辑表达式进行化简,要综合使用上述技巧。以下再举几例。
2.1.7 化简I∶=AD+AD+AB+AC+BD+A BEF+BEF。
解: L=A+AB+C+BD+A引叩+BEF (A+A=1)
=A+AC+BD+BEF (利用A+AB=A)
=A+C+BD+BEF (利用A+AB=A+B)
例2.1.8 已知逻辑函数表达式为L=ABD+ABD+ABD+ABCD
最简的与一或逻辑函数表达式。并画出相应的逻辑图;
仅用与非门画出最简表达式的逻辑图。
解: L=AB(D+D)+ABD+9(C+C)
=AB+1B(~D+D)
=AB+AB (与一或表达式)
VI-21W-EY数字密码锁内部由8个拨动开关设置了8位二进制密码,分别用D7、D6、D5、D4、D3、D2、D1、DO表示。开锁时的串行输人数码由BFr开关产生,可以为0或1,如图10.2.13所示,为了使系统REr能1位1位地依次读取由Brr开关送来的串行数码,设置了1个按钮开关RmD,送入数码 my时,首先用Brr开关设置1位数码,然后按下RE'DRE4D开关,这样就将Brr开关产生的当前数Brr码读入系统。为了标识串行数码输入开始和结束,设置了RESEr和「Ry按钮开关,RESEr
信号使系统进入初始状态,准备接受新的串行数码,当送8位数码与开锁密码一致时,按下图10.2.13 数字锁框图rRy产生开锁信号,系统便输出0PEⅣ信号打开锁,否则数字锁不开,并输出错误信号ERROR。

将系统划分为控制单元和处理单元,将数字密码锁划分为控制单元和处理单元两部分如图10.2.14所示,控制单元控制处理单元接受Brr产生的数码,并将其与对应的密码位相比较,比较结果召作为状态信息送到控制单元。为累计输人数码的位数,需要一个计数器。控制单元发出的控制信号C乙R使计数器清零,并使数码的比较从低位开利用A+AB=A的公式,消去多余的项AB。根据代入规则,A、B可以是任何一个复杂的逻辑式。
例2.1.4 试用吸收法化简逻辑函数表达式山=处B+ABCDE+ABCDF。
解: u=AB+ABCI9(E+F)=AB
消去法,利用A+AB=⒕+B,消去多余的因子。
例2.1.5 试用消去法化简逻辑函数表达式乙=AB+AC+BC。
解: u=AB+(A+B)C
=AB+aBC
=AB+C
配项法,先利用A=△(B+B),增加必要的乘积项,再用并项或吸收的办法使项数
减少。
例2,1.6 试用配项法化简逻辑函数表达式L=AB+AC+BC。
解: u=AB+AC+(A+A)BC
=AB+AC+AB C+AB C
=(AB+AB C)+(AC+AC)B)
=AB+AC
使用配项的方法要有一定的经验,否则越配越繁。通常对逻辑表达式进行化简,要综合使用上述技巧。以下再举几例。

2.1.7 化简I∶=AD+AD+AB+AC+BD+A BEF+BEF。
解: L=A+AB+C+BD+A引叩+BEF (A+A=1)
=A+AC+BD+BEF (利用A+AB=A)
=A+C+BD+BEF (利用A+AB=A+B)
例2.1.8 已知逻辑函数表达式为L=ABD+ABD+ABD+ABCD
最简的与一或逻辑函数表达式。并画出相应的逻辑图;
仅用与非门画出最简表达式的逻辑图。
解: L=AB(D+D)+ABD+9(C+C)
=AB+1B(~D+D)
=AB+AB (与一或表达式)
上一篇:WP4C1 计数器清零端
上一篇:TLV1544I数字锁系统




 公网安备44030402000607
公网安备44030402000607





